Estimating location parameters in entangled single-sample distributions
Paper and Code
Jul 06, 2019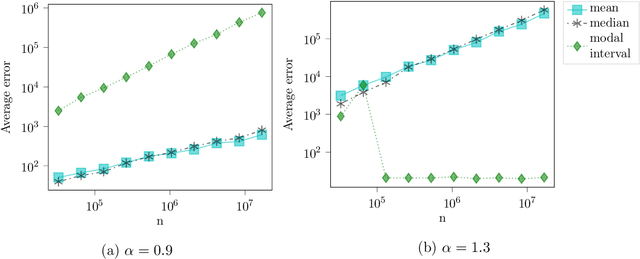
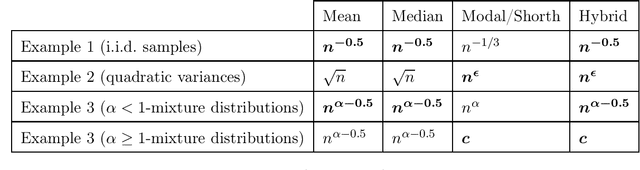

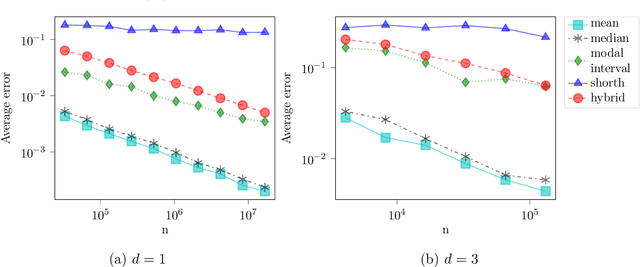
We consider the problem of estimating the common mean of independently sampled data, where samples are drawn in a possibly non-identical manner from symmetric, unimodal distributions with a common mean. This generalizes the setting of Gaussian mixture modeling, since the number of distinct mixture components may diverge with the number of observations. We propose an estimator that adapts to the level of heterogeneity in the data, achieving near-optimality in both the i.i.d. setting and some heterogeneous settings, where the fraction of ``low-noise'' points is as small as $\frac{\log n}{n}$. Our estimator is a hybrid of the modal interval, shorth, and median estimators from classical statistics; however, the key technical contributions rely on novel empirical process theory results that we derive for independent but non-i.i.d. data. In the multivariate setting, we generalize our theory to mean estimation for mixtures of radially symmetric distributions, and derive minimax lower bounds on the expected error of any estimator that is agnostic to the scales of individual data points. Finally, we describe an extension of our estimators applicable to linear regression. In the multivariate mean estimation and regression settings, we present computationally feasible versions of our estimators that run in time polynomial in the number of data points.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge