Privacy Amplification by Decentralization

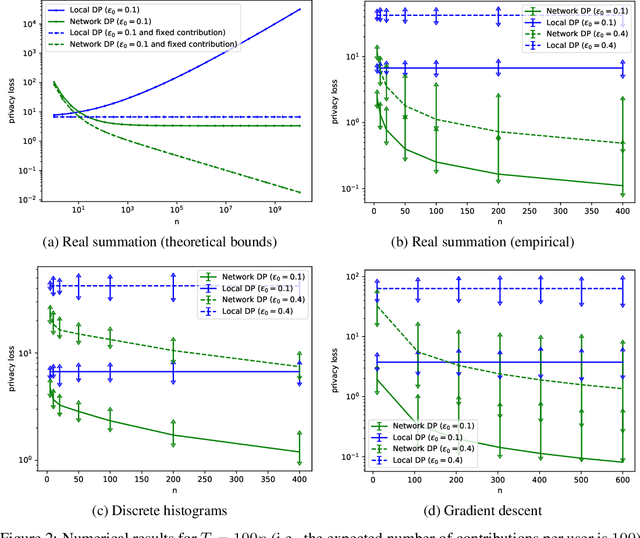
Analyzing data owned by several parties while achieving a good trade-off between utility and privacy is a key challenge in federated learning and analytics. In this work, we introduce a novel relaxation of local differential privacy (LDP) that naturally arises in fully decentralized protocols, i.e. participants exchange information by communicating along the edges of a network graph. This relaxation, that we call network DP, captures the fact that users have only a local view of the decentralized system. To show the relevance of network DP, we study a decentralized model of computation where a token performs a walk on the network graph and is updated sequentially by the party who receives it. For tasks such as real summation, histogram computation and gradient descent, we propose simple algorithms and prove privacy amplification results on ring and complete topologies. The resulting privacy-utility trade-off significantly improves upon LDP, and in some cases even matches what can be achieved with approaches based on secure aggregation and secure shuffling. Our experiments confirm the practical significance of the gains compared to LDP.