Alireza Bagheri Garakani
Multi-objective Ranking via Constrained Optimization
Feb 13, 2020
Abstract:In this paper, we introduce an Augmented Lagrangian based method to incorporate the multiple objectives (MO) in a search ranking algorithm. Optimizing MOs is an essential and realistic requirement for building ranking models in production. The proposed method formulates MO in constrained optimization and solves the problem in the popular Boosting framework -- a novel contribution of our work. Furthermore, we propose a procedure to set up all optimization parameters in the problem. The experimental results show that the method successfully achieves MO criteria much more efficiently than existing methods.
Kernel Approximation Methods for Speech Recognition
Jan 13, 2017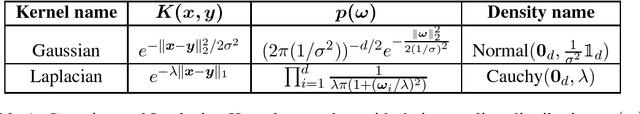
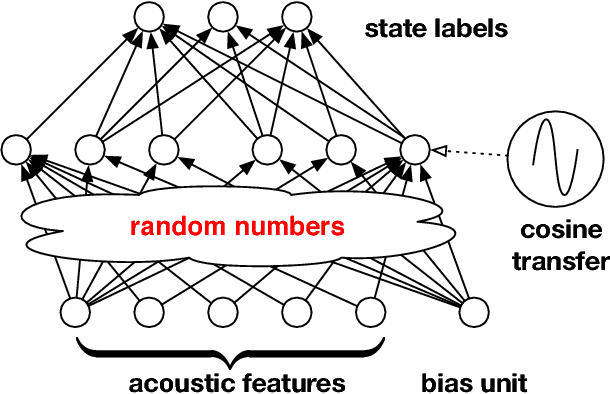
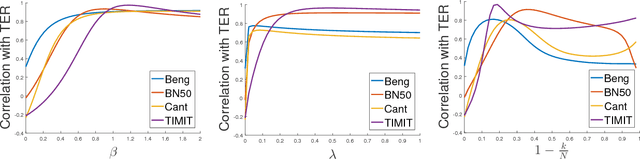

Abstract:We study large-scale kernel methods for acoustic modeling in speech recognition and compare their performance to deep neural networks (DNNs). We perform experiments on four speech recognition datasets, including the TIMIT and Broadcast News benchmark tasks, and compare these two types of models on frame-level performance metrics (accuracy, cross-entropy), as well as on recognition metrics (word/character error rate). In order to scale kernel methods to these large datasets, we use the random Fourier feature method of Rahimi and Recht (2007). We propose two novel techniques for improving the performance of kernel acoustic models. First, in order to reduce the number of random features required by kernel models, we propose a simple but effective method for feature selection. The method is able to explore a large number of non-linear features while maintaining a compact model more efficiently than existing approaches. Second, we present a number of frame-level metrics which correlate very strongly with recognition performance when computed on the heldout set; we take advantage of these correlations by monitoring these metrics during training in order to decide when to stop learning. This technique can noticeably improve the recognition performance of both DNN and kernel models, while narrowing the gap between them. Additionally, we show that the linear bottleneck method of Sainath et al. (2013) improves the performance of our kernel models significantly, in addition to speeding up training and making the models more compact. Together, these three methods dramatically improve the performance of kernel acoustic models, making their performance comparable to DNNs on the tasks we explored.
A Comparison between Deep Neural Nets and Kernel Acoustic Models for Speech Recognition
Mar 18, 2016


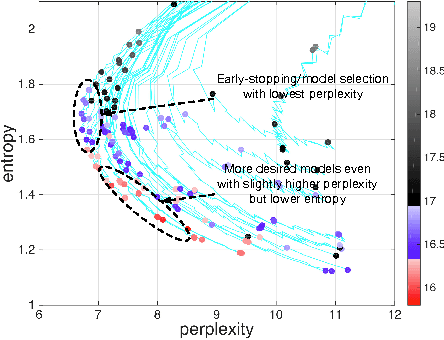
Abstract:We study large-scale kernel methods for acoustic modeling and compare to DNNs on performance metrics related to both acoustic modeling and recognition. Measuring perplexity and frame-level classification accuracy, kernel-based acoustic models are as effective as their DNN counterparts. However, on token-error-rates DNN models can be significantly better. We have discovered that this might be attributed to DNN's unique strength in reducing both the perplexity and the entropy of the predicted posterior probabilities. Motivated by our findings, we propose a new technique, entropy regularized perplexity, for model selection. This technique can noticeably improve the recognition performance of both types of models, and reduces the gap between them. While effective on Broadcast News, this technique could be also applicable to other tasks.
How to Scale Up Kernel Methods to Be As Good As Deep Neural Nets
Jun 17, 2015



Abstract:The computational complexity of kernel methods has often been a major barrier for applying them to large-scale learning problems. We argue that this barrier can be effectively overcome. In particular, we develop methods to scale up kernel models to successfully tackle large-scale learning problems that are so far only approachable by deep learning architectures. Based on the seminal work by Rahimi and Recht on approximating kernel functions with features derived from random projections, we advance the state-of-the-art by proposing methods that can efficiently train models with hundreds of millions of parameters, and learn optimal representations from multiple kernels. We conduct extensive empirical studies on problems from image recognition and automatic speech recognition, and show that the performance of our kernel models matches that of well-engineered deep neural nets (DNNs). To the best of our knowledge, this is the first time that a direct comparison between these two methods on large-scale problems is reported. Our kernel methods have several appealing properties: training with convex optimization, cost for training a single model comparable to DNNs, and significantly reduced total cost due to fewer hyperparameters to tune for model selection. Our contrastive study between these two very different but equally competitive models sheds light on fundamental questions such as how to learn good representations.
A Distributed Frank-Wolfe Algorithm for Communication-Efficient Sparse Learning
Jan 12, 2015



Abstract:Learning sparse combinations is a frequent theme in machine learning. In this paper, we study its associated optimization problem in the distributed setting where the elements to be combined are not centrally located but spread over a network. We address the key challenges of balancing communication costs and optimization errors. To this end, we propose a distributed Frank-Wolfe (dFW) algorithm. We obtain theoretical guarantees on the optimization error $\epsilon$ and communication cost that do not depend on the total number of combining elements. We further show that the communication cost of dFW is optimal by deriving a lower-bound on the communication cost required to construct an $\epsilon$-approximate solution. We validate our theoretical analysis with empirical studies on synthetic and real-world data, which demonstrate that dFW outperforms both baselines and competing methods. We also study the performance of dFW when the conditions of our analysis are relaxed, and show that dFW is fairly robust.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge