When adversarial attacks become interpretable counterfactual explanations
Paper and Code
Jun 14, 2022
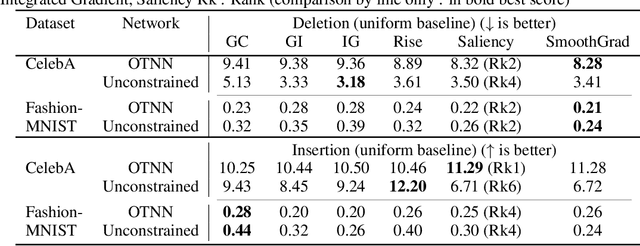
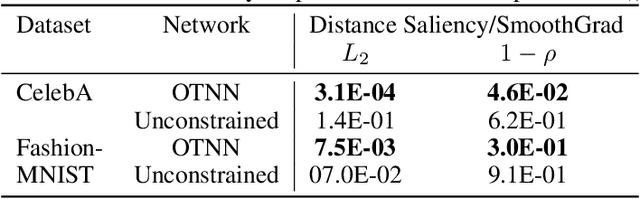
We argue that, when learning a 1-Lipschitz neural network with the dual loss of an optimal transportation problem, the gradient of the model is both the direction of the transportation plan and the direction to the closest adversarial attack. Traveling along the gradient to the decision boundary is no more an adversarial attack but becomes a counterfactual explanation, explicitly transporting from one class to the other. Through extensive experiments on XAI metrics, we find that the simple saliency map method, applied on such networks, becomes a reliable explanation, and outperforms the state-of-the-art explanation approaches on unconstrained models. The proposed networks were already known to be certifiably robust, and we prove that they are also explainable with a fast and simple method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge