Understanding black-box models with dependent inputs through a generalization of Hoeffding's decomposition

One of the main challenges for interpreting black-box models is the ability to uniquely decompose square-integrable functions of non-mutually independent random inputs into a sum of functions of every possible subset of variables. However, dealing with dependencies among inputs can be complicated. We propose a novel framework to study this problem, linking three domains of mathematics: probability theory, functional analysis, and combinatorics. We show that, under two reasonable assumptions on the inputs (non-perfect functional dependence and non-degenerate stochastic dependence), it is always possible to decompose uniquely such a function. This ``canonical decomposition'' is relatively intuitive and unveils the linear nature of non-linear functions of non-linearly dependent inputs. In this framework, we effectively generalize the well-known Hoeffding decomposition, which can be seen as a particular case. Oblique projections of the black-box model allow for novel interpretability indices for evaluation and variance decomposition. Aside from their intuitive nature, the properties of these novel indices are studied and discussed. This result offers a path towards a more precise uncertainty quantification, which can benefit sensitivity analyses and interpretability studies, whenever the inputs are dependent. This decomposition is illustrated analytically, and the challenges to adopting these results in practice are discussed.

Quantile-constrained Wasserstein projections for robust interpretability of numerical and machine learning models

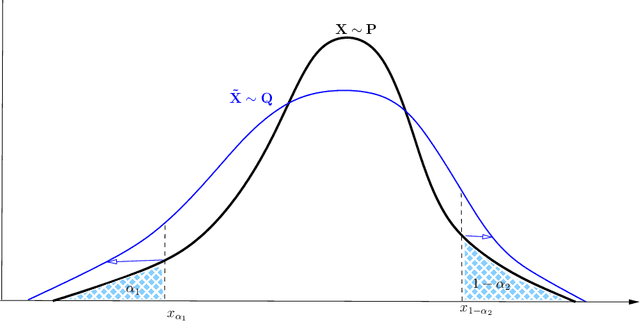
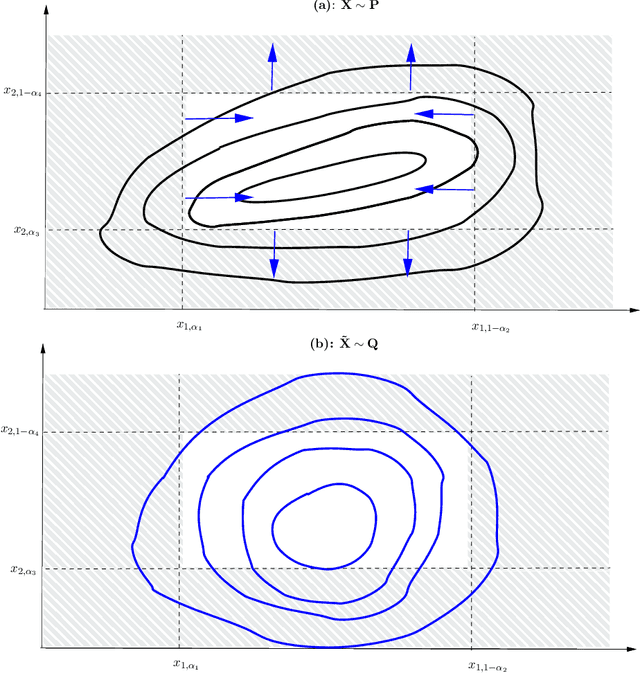
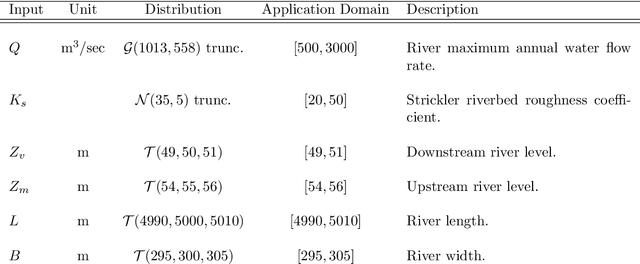
Robustness studies of black-box models is recognized as a necessary task for numerical models based on structural equations and predictive models learned from data. These studies must assess the model's robustness to possible misspecification of regarding its inputs (e.g., covariate shift). The study of black-box models, through the prism of uncertainty quantification (UQ), is often based on sensitivity analysis involving a probabilistic structure imposed on the inputs, while ML models are solely constructed from observed data. Our work aim at unifying the UQ and ML interpretability approaches, by providing relevant and easy-to-use tools for both paradigms. To provide a generic and understandable framework for robustness studies, we define perturbations of input information relying on quantile constraints and projections with respect to the Wasserstein distance between probability measures, while preserving their dependence structure. We show that this perturbation problem can be analytically solved. Ensuring regularity constraints by means of isotonic polynomial approximations leads to smoother perturbations, which can be more suitable in practice. Numerical experiments on real case studies, from the UQ and ML fields, highlight the computational feasibility of such studies and provide local and global insights on the robustness of black-box models to input perturbations.