Concave Statistical Utility Maximization Bandits via Influence-Function Gradients

We study stochastic multi-armed bandits in which the objective is a statistical functional of the long-run reward distribution, rather than expected reward alone. Under mild continuity assumptions, we show that the infinite-horizon problem reduces to optimizing over stationary mixed policies: each weight vector \(w\) on the simplex induces a mixture law \(P^w\), and performance is measured by the concave utility \(U(w)=\mathfrak U(P^w)\). For differentiable statistical utilities, we use influence-function calculus to derive stochastic gradient estimators from bandit feedback. This leads to an entropic mirror-ascent algorithm on a truncated simplex, implemented through multiplicative-weights updates and plug-in estimates of the influence function. We establish regret bounds that separate the mirror-ascent optimization error from the bias caused by estimating the influence function. The framework is developed for general concave distributional utilities and illustrated through variance and Wasserstein objectives, with numerical experiments comparing exact and plug-in influence-function implementations.

Conformal Robust Set Estimation

Conformal prediction provides finite-sample, distribution-free coverage under exchangeability, but standard constructions may lack robustness in the presence of outliers or heavy tails. We propose a robust conformal method based on a non-conformity score defined as the half-mass radius around a point, equivalently the distance to its $(\lfloor n/2\rfloor+1)$-nearest neighbour. We show that the resulting conformal regions are marginally valid for any sample size and converge in probability to a robust population central set defined through a distance-to-a-measure functional. Under mild regularity conditions, we establish exponential concentration and tail bounds that quantify the deviation between the empirical conformal region and its population counterpart. These results provide a probabilistic justification for using robust geometric scores in conformal prediction, even for heavy-tailed or multi-modal distributions.

On consistent estimation of dimension values

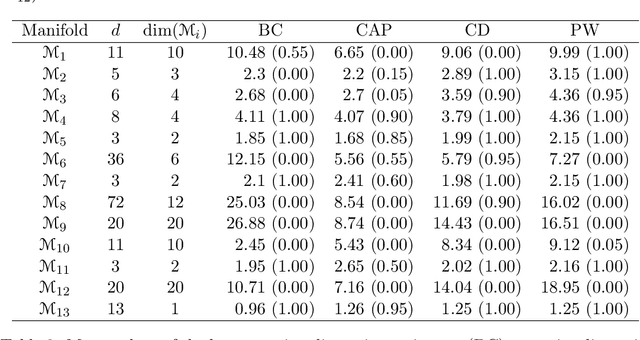
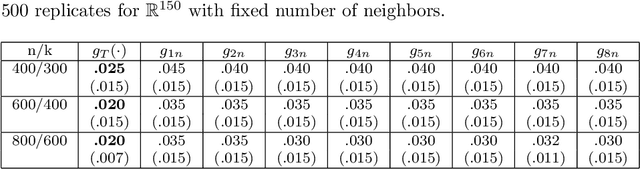
The problem of estimating, from a random sample of points, the dimension of a compact subset S of the Euclidean space is considered. The emphasis is put on consistency results in the statistical sense. That is, statements of convergence to the true dimension value when the sample size grows to infinity. Among the many available definitions of dimension, we have focused (on the grounds of its statistical tractability) on three notions: the Minkowski dimension, the correlation dimension and the, perhaps less popular, concept of pointwise dimension. We prove the statistical consistency of some natural estimators of these quantities. Our proofs partially rely on the use of an instrumental estimator formulated in terms of the empirical volume function Vn (r), defined as the Lebesgue measure of the set of points whose distance to the sample is at most r. In particular, we explore the case in which the true volume function V (r) of the target set S is a polynomial on some interval starting at zero. An empirical study is also included. Our study aims to provide some theoretical support, and some practical insights, for the problem of deciding whether or not the set S has a dimension smaller than that of the ambient space. This is a major statistical motivation of the dimension studies, in connection with the so-called Manifold Hypothesis.

GROS: A General Robust Aggregation Strategy

A new, very general, robust procedure for combining estimators in metric spaces is introduced GROS. The method is reminiscent of the well-known median of means, as described in \cite{devroye2016sub}. Initially, the sample is divided into $K$ groups. Subsequently, an estimator is computed for each group. Finally, these $K$ estimators are combined using a robust procedure. We prove that this estimator is sub-Gaussian and we get its break-down point, in the sense of Donoho. The robust procedure involves a minimization problem on a general metric space, but we show that the same (up to a constant) sub-Gaussianity is obtained if the minimization is taken over the sample, making GROS feasible in practice. The performance of GROS is evaluated through five simulation studies: the first one focuses on classification using $k$-means, the second one on the multi-armed bandit problem, the third one on the regression problem. The fourth one is the set estimation problem under a noisy model. Lastly, we apply GROS to get a robust persistent diagram.

Conformal inference for regression on Riemannian Manifolds

Regression on manifolds, and, more broadly, statistics on manifolds, has garnered significant importance in recent years due to the vast number of applications for this type of data. Circular data is a classic example, but so is data in the space of covariance matrices, data on the Grassmannian manifold obtained as a result of principal component analysis, among many others. In this work we investigate prediction sets for regression scenarios when the response variable, denoted by $Y$, resides in a manifold, and the covariable, denoted by X, lies in Euclidean space. This extends the concepts delineated in [Lei and Wasserman, 2014] to this novel context. Aligning with traditional principles in conformal inference, these prediction sets are distribution-free, indicating that no specific assumptions are imposed on the joint distribution of $(X, Y)$, and they maintain a non-parametric character. We prove the asymptotic almost sure convergence of the empirical version of these regions on the manifold to their population counterparts. The efficiency of this method is shown through a comprehensive simulation study and an analysis involving real-world data.

Semi-supervised learning: When and why it works

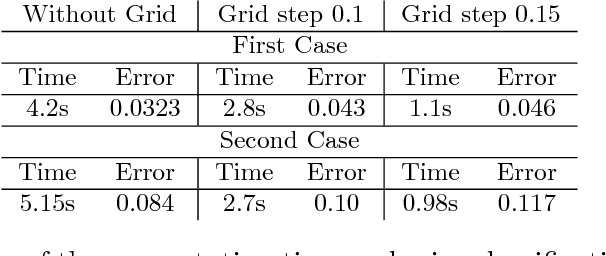
Semi-supervised learning deals with the problem of how, if possible, to take advantage of a huge amount of unclassified data, to perform a classification in situations when, typically, there is little labelled data. Even though this is not always possible (it depends on how useful, for inferring the labels, it would be to know the distribution of the unlabelled data), several algorithm have been proposed recently. A new algorithm is proposed, that under almost necessary conditions, attains asymptotically the performance of the best theoretical rule as the amount of unlabelled data tends to infinity. The set of necessary assumptions, although reasonable, show that semi-parametric classi- fication only works for very well conditioned problems. The perfor- mance of the algorithm is assessed in the well known "Isolet" real-data of phonemes, where a strong dependence on the choice of the initial training sample is shown.

Semi-supervised learning

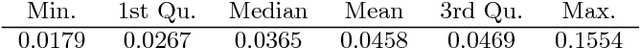
Semi-supervised learning deals with the problem of how, if possible, to take advantage of a huge amount of not classified data, to perform classification, in situations when, typically, the labelled data are few. Even though this is not always possible (it depends on how useful is to know the distribution of the unlabelled data in the inference of the labels), several algorithm have been proposed recently. A new algorithm is proposed, that under almost neccesary conditions, attains asymptotically the performance of the best theoretical rule, when the size of unlabeled data tends to infinity. The set of necessary assumptions, although reasonables, show that semi-parametric classification only works for very well conditioned problems.

A nonlinear aggregation type classifier

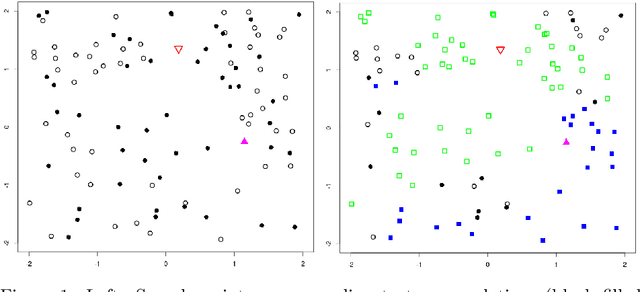
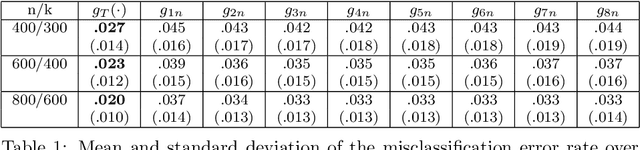
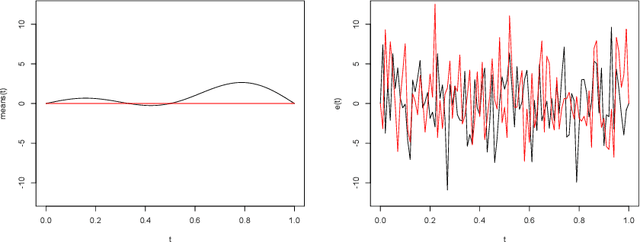
We introduce a nonlinear aggregation type classifier for functional data defined on a separable and complete metric space. The new rule is built up from a collection of $M$ arbitrary training classifiers. If the classifiers are consistent, then so is the aggregation rule. Moreover, asymptotically the aggregation rule behaves as well as the best of the $M$ classifiers. The results of a small simulation are reported both, for high dimensional and functional data, and a real data example is analyzed.