A nonlinear aggregation type classifier
Paper and Code
Sep 09, 2015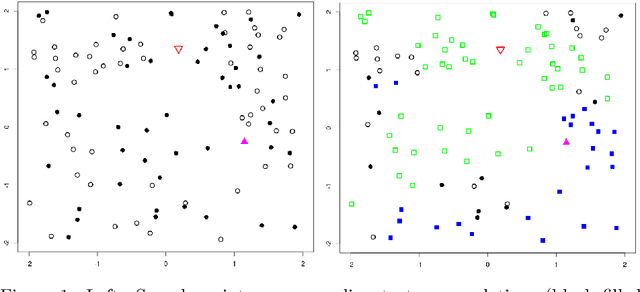
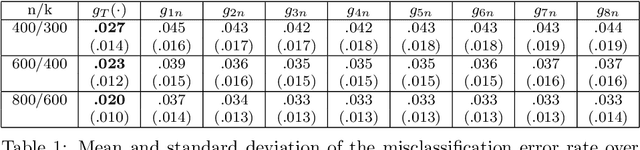
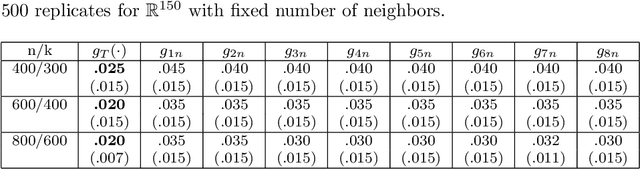
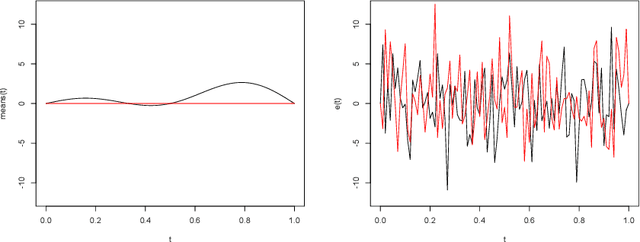
We introduce a nonlinear aggregation type classifier for functional data defined on a separable and complete metric space. The new rule is built up from a collection of $M$ arbitrary training classifiers. If the classifiers are consistent, then so is the aggregation rule. Moreover, asymptotically the aggregation rule behaves as well as the best of the $M$ classifiers. The results of a small simulation are reported both, for high dimensional and functional data, and a real data example is analyzed.
* arXiv admin note: text overlap with arXiv:1411.2687
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge