Semi-supervised learning

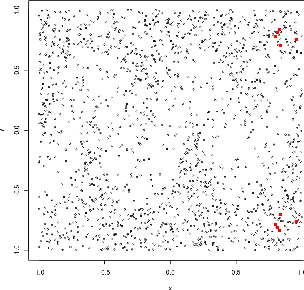
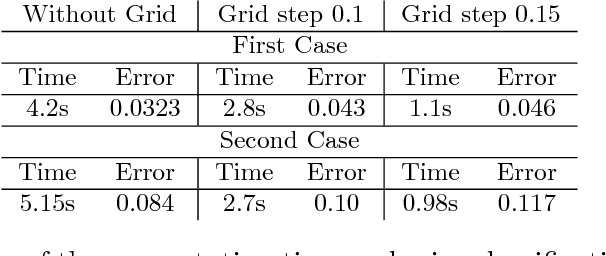
Semi-supervised learning deals with the problem of how, if possible, to take advantage of a huge amount of not classified data, to perform classification, in situations when, typically, the labelled data are few. Even though this is not always possible (it depends on how useful is to know the distribution of the unlabelled data in the inference of the labels), several algorithm have been proposed recently. A new algorithm is proposed, that under almost neccesary conditions, attains asymptotically the performance of the best theoretical rule, when the size of unlabeled data tends to infinity. The set of necessary assumptions, although reasonables, show that semi-parametric classification only works for very well conditioned problems.

A nonlinear aggregation type classifier

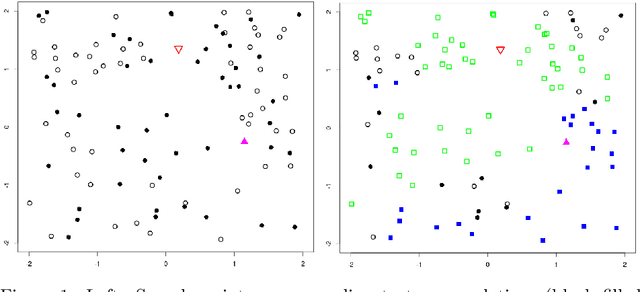
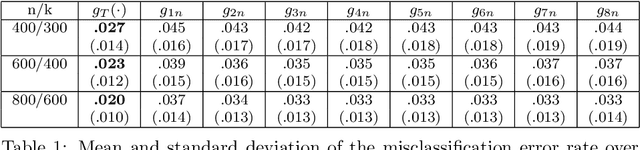
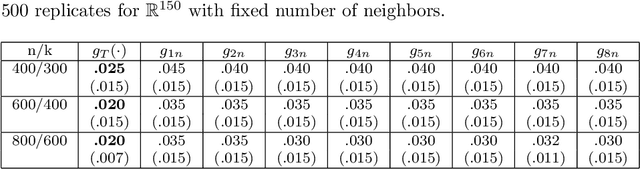
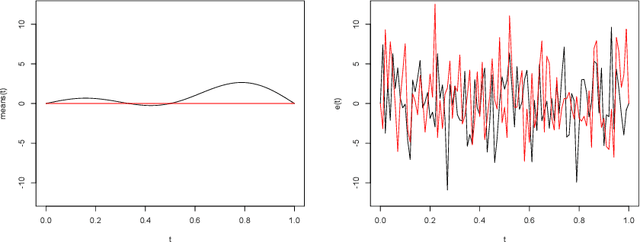
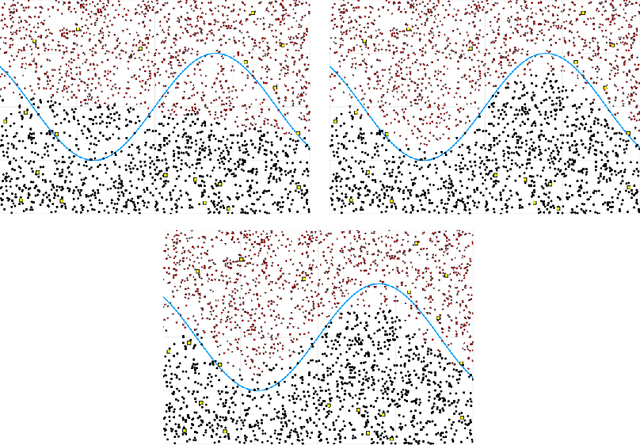
We introduce a nonlinear aggregation type classifier for functional data defined on a separable and complete metric space. The new rule is built up from a collection of $M$ arbitrary training classifiers. If the classifiers are consistent, then so is the aggregation rule. Moreover, asymptotically the aggregation rule behaves as well as the best of the $M$ classifiers. The results of a small simulation are reported both, for high dimensional and functional data, and a real data example is analyzed.

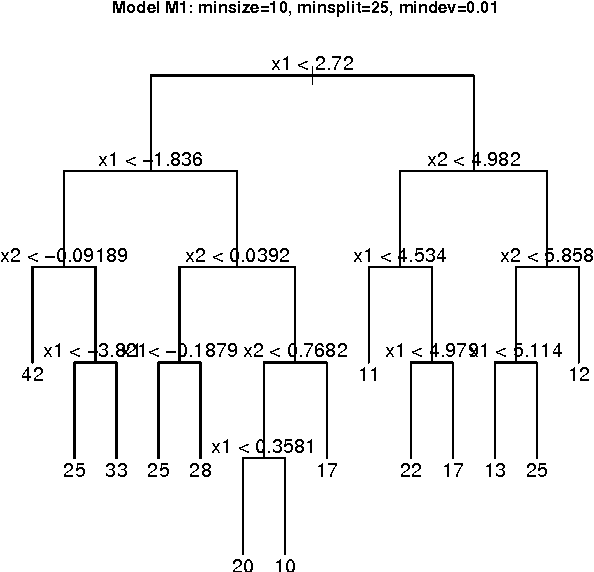
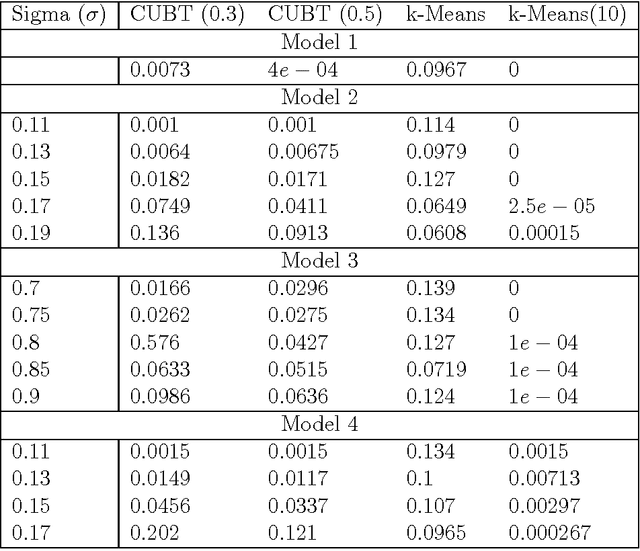
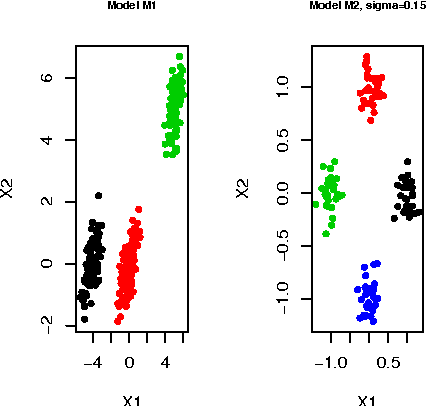
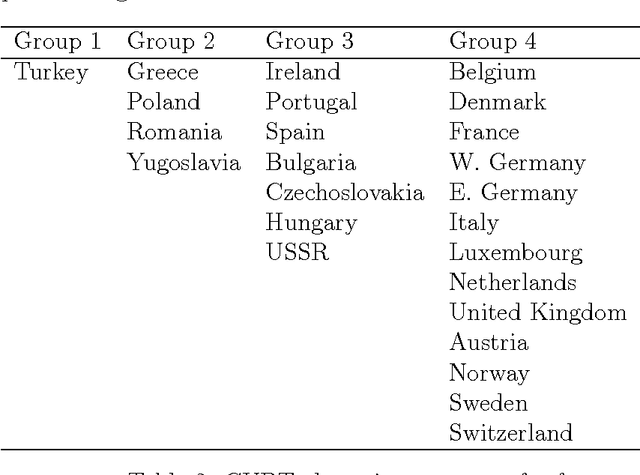
Clustering using Unsupervised Binary Trees: CUBT

We herein introduce a new method of interpretable clustering that uses unsupervised binary trees. It is a three-stage procedure, the first stage of which entails a series of recursive binary splits to reduce the heterogeneity of the data within the new subsamples. During the second stage (pruning), consideration is given to whether adjacent nodes can be aggregated. Finally, during the third stage (joining), similar clusters are joined together, even if they do not share the same parent originally. Consistency results are obtained, and the procedure is used on simulated and real data sets.