On consistent estimation of dimension values

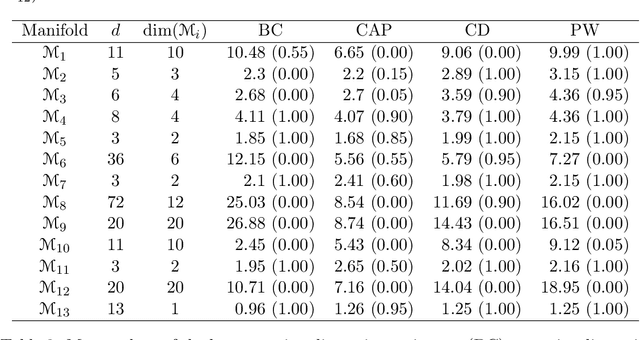
The problem of estimating, from a random sample of points, the dimension of a compact subset S of the Euclidean space is considered. The emphasis is put on consistency results in the statistical sense. That is, statements of convergence to the true dimension value when the sample size grows to infinity. Among the many available definitions of dimension, we have focused (on the grounds of its statistical tractability) on three notions: the Minkowski dimension, the correlation dimension and the, perhaps less popular, concept of pointwise dimension. We prove the statistical consistency of some natural estimators of these quantities. Our proofs partially rely on the use of an instrumental estimator formulated in terms of the empirical volume function Vn (r), defined as the Lebesgue measure of the set of points whose distance to the sample is at most r. In particular, we explore the case in which the true volume function V (r) of the target set S is a polynomial on some interval starting at zero. An empirical study is also included. Our study aims to provide some theoretical support, and some practical insights, for the problem of deciding whether or not the set S has a dimension smaller than that of the ambient space. This is a major statistical motivation of the dimension studies, in connection with the so-called Manifold Hypothesis.

On uniqueness of the set of k-means

We provide necessary and sufficient conditions for the uniqueness of the k-means set of a probability distribution. This uniqueness problem is related to the choice of k: depending on the underlying distribution, some values of this parameter could lead to multiple sets of k-means, which hampers the interpretation of the results and/or the stability of the algorithms. We give a general assessment on consistency of the empirical k-means adapted to the setting of non-uniqueness and determine the asymptotic distribution of the within cluster sum of squares (WCSS). We also provide statistical characterizations of k-means uniqueness in terms of the asymptotic behavior of the empirical WCSS. As a consequence, we derive a bootstrap test for uniqueness of the set of k-means. The results are illustrated with examples of different types of non-uniqueness and we check by simulations the performance of the proposed methodology.

The mRMR variable selection method: a comparative study for functional data

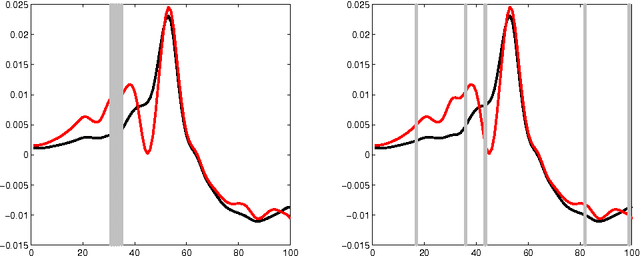
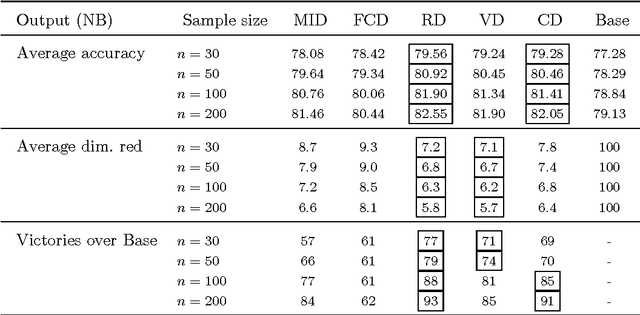
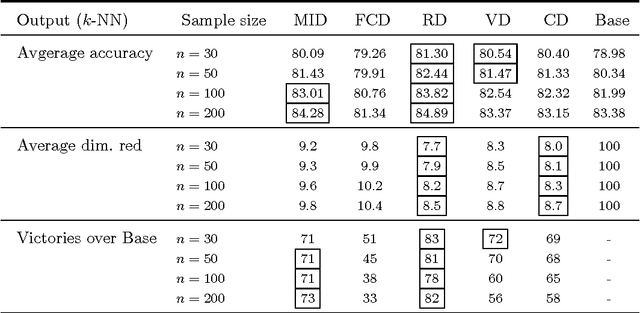
The use of variable selection methods is particularly appealing in statistical problems with functional data. The obvious general criterion for variable selection is to choose the `most representative' or `most relevant' variables. However, it is also clear that a purely relevance-oriented criterion could lead to select many redundant variables. The mRMR (minimum Redundance Maximum Relevance) procedure, proposed by Ding and Peng (2005) and Peng et al. (2005) is an algorithm to systematically perform variable selection, achieving a reasonable trade-off between relevance and redundancy. In its original form, this procedure is based on the use of the so-called mutual information criterion to assess relevance and redundancy. Keeping the focus on functional data problems, we propose here a modified version of the mRMR method, obtained by replacing the mutual information by the new association measure (called distance correlation) suggested by Sz\'ekely et al. (2007). We have also performed an extensive simulation study, including 1600 functional experiments (100 functional models $\times$ 4 sample sizes $\times$ 4 classifiers) and three real-data examples aimed at comparing the different versions of the mRMR methodology. The results are quite conclusive in favor of the new proposed alternative.

Supervised classification for a family of Gaussian functional models

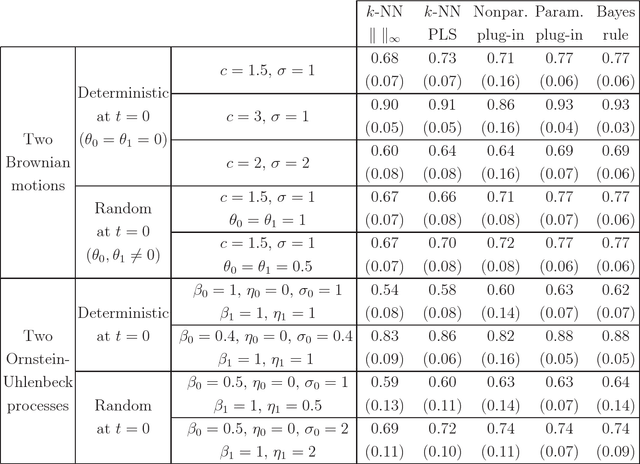
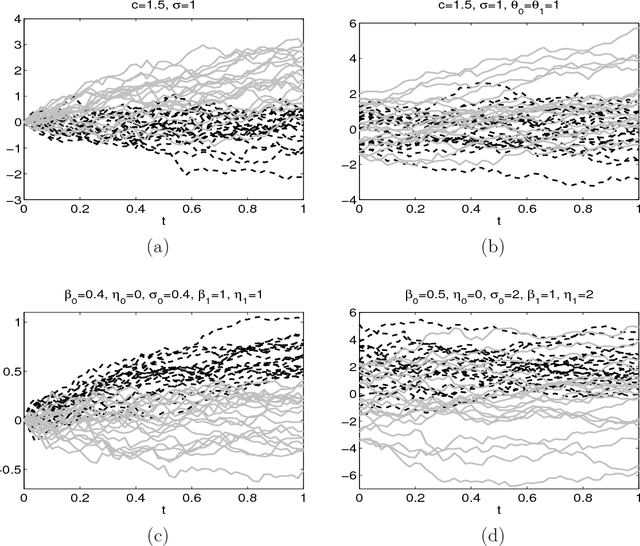
In the framework of supervised classification (discrimination) for functional data, it is shown that the optimal classification rule can be explicitly obtained for a class of Gaussian processes with "triangular" covariance functions. This explicit knowledge has two practical consequences. First, the consistency of the well-known nearest neighbors classifier (which is not guaranteed in the problems with functional data) is established for the indicated class of processes. Second, and more important, parametric and nonparametric plug-in classifiers can be obtained by estimating the unknown elements in the optimal rule. The performance of these new plug-in classifiers is checked, with positive results, through a simulation study and a real data example.

Supervised functional classification: A theoretical remark and some comparisons

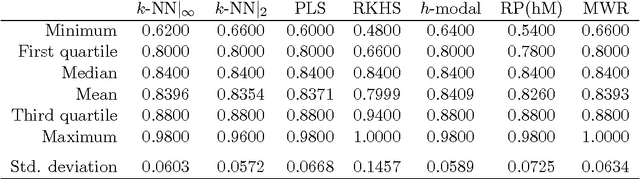
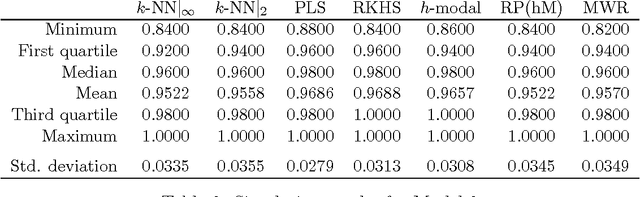
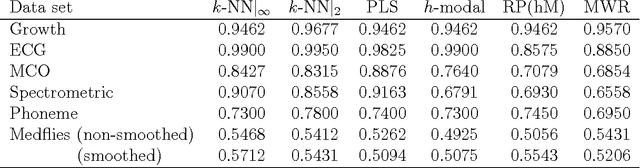
The problem of supervised classification (or discrimination) with functional data is considered, with a special interest on the popular k-nearest neighbors (k-NN) classifier. First, relying on a recent result by Cerou and Guyader (2006), we prove the consistency of the k-NN classifier for functional data whose distribution belongs to a broad family of Gaussian processes with triangular covariance functions. Second, on a more practical side, we check the behavior of the k-NN method when compared with a few other functional classifiers. This is carried out through a small simulation study and the analysis of several real functional data sets. While no global "uniform" winner emerges from such comparisons, the overall performance of the k-NN method, together with its sound intuitive motivation and relative simplicity, suggests that it could represent a reasonable benchmark for the classification problem with functional data.