Supervised classification for a family of Gaussian functional models
Paper and Code
Apr 28, 2010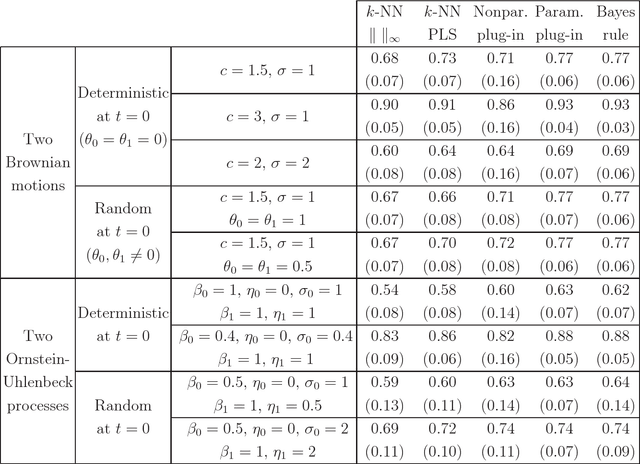
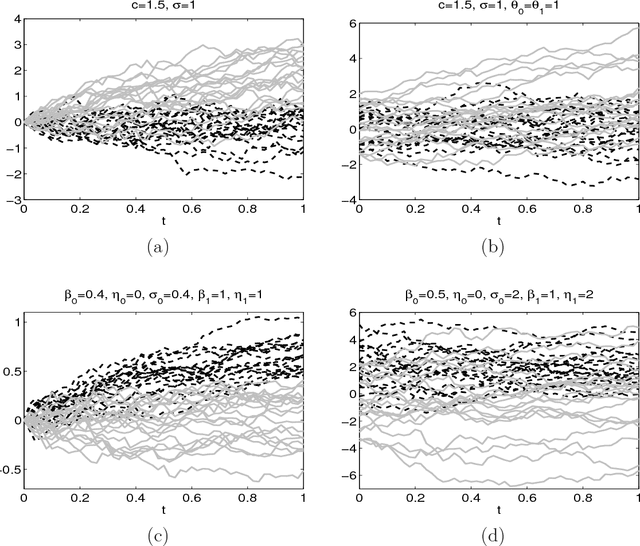

In the framework of supervised classification (discrimination) for functional data, it is shown that the optimal classification rule can be explicitly obtained for a class of Gaussian processes with "triangular" covariance functions. This explicit knowledge has two practical consequences. First, the consistency of the well-known nearest neighbors classifier (which is not guaranteed in the problems with functional data) is established for the indicated class of processes. Second, and more important, parametric and nonparametric plug-in classifiers can be obtained by estimating the unknown elements in the optimal rule. The performance of these new plug-in classifiers is checked, with positive results, through a simulation study and a real data example.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge