Relation between PLS and OLS regression in terms of the eigenvalue distribution of the regressor covariance matrix

Partial least squares (PLS) is a dimensionality reduction technique introduced in the field of chemometrics and successfully employed in many other areas. The PLS components are obtained by maximizing the covariance between linear combinations of the regressors and of the target variables. In this work, we focus on its application to scalar regression problems. PLS regression consists in finding the least squares predictor that is a linear combination of a subset of the PLS components. Alternatively, PLS regression can be formulated as a least squares problem restricted to a Krylov subspace. This equivalent formulation is employed to analyze the distance between ${\hat{\boldsymbol\beta}\;}_{\mathrm{PLS}}^{\scriptscriptstyle {(L)}}$, the PLS estimator of the vector of coefficients of the linear regression model based on $L$ PLS components, and $\hat{\boldsymbol \beta}_{\mathrm{OLS}}$, the one obtained by ordinary least squares (OLS), as a function of $L$. Specifically, ${\hat{\boldsymbol\beta}\;}_{\mathrm{PLS}}^{\scriptscriptstyle {(L)}}$ is the vector of coefficients in the aforementioned Krylov subspace that is closest to $\hat{\boldsymbol \beta}_{\mathrm{OLS}}$ in terms of the Mahalanobis distance with respect to the covariance matrix of the OLS estimate. We provide a bound on this distance that depends only on the distribution of the eigenvalues of the regressor covariance matrix. Numerical examples on synthetic and real-world data are used to illustrate how the distance between ${\hat{\boldsymbol\beta}\;}_{\mathrm{PLS}}^{\scriptscriptstyle {(L)}}$ and $\hat{\boldsymbol \beta}_{\mathrm{OLS}}$ depends on the number of clusters in which the eigenvalues of the regressor covariance matrix are grouped.

The mRMR variable selection method: a comparative study for functional data

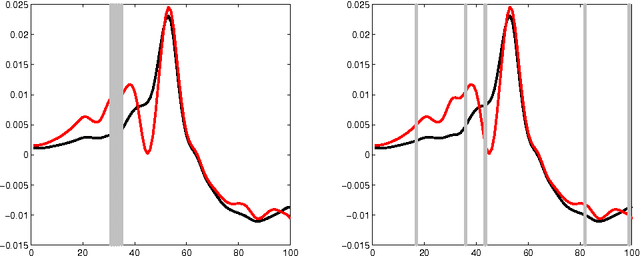
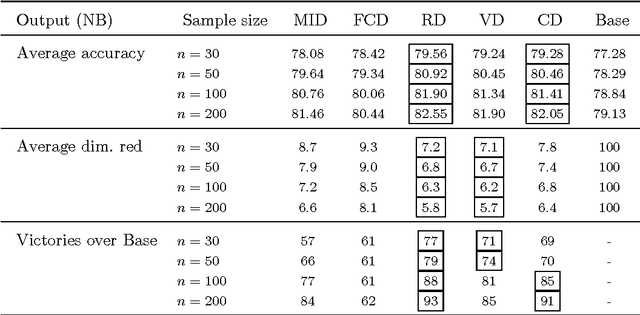
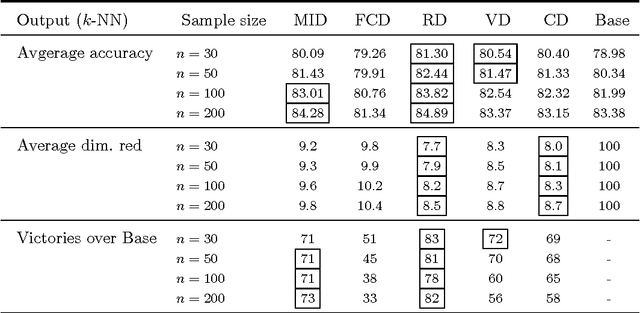
The use of variable selection methods is particularly appealing in statistical problems with functional data. The obvious general criterion for variable selection is to choose the `most representative' or `most relevant' variables. However, it is also clear that a purely relevance-oriented criterion could lead to select many redundant variables. The mRMR (minimum Redundance Maximum Relevance) procedure, proposed by Ding and Peng (2005) and Peng et al. (2005) is an algorithm to systematically perform variable selection, achieving a reasonable trade-off between relevance and redundancy. In its original form, this procedure is based on the use of the so-called mutual information criterion to assess relevance and redundancy. Keeping the focus on functional data problems, we propose here a modified version of the mRMR method, obtained by replacing the mutual information by the new association measure (called distance correlation) suggested by Sz\'ekely et al. (2007). We have also performed an extensive simulation study, including 1600 functional experiments (100 functional models $\times$ 4 sample sizes $\times$ 4 classifiers) and three real-data examples aimed at comparing the different versions of the mRMR methodology. The results are quite conclusive in favor of the new proposed alternative.