Relation between PLS and OLS regression in terms of the eigenvalue distribution of the regressor covariance matrix

Partial least squares (PLS) is a dimensionality reduction technique introduced in the field of chemometrics and successfully employed in many other areas. The PLS components are obtained by maximizing the covariance between linear combinations of the regressors and of the target variables. In this work, we focus on its application to scalar regression problems. PLS regression consists in finding the least squares predictor that is a linear combination of a subset of the PLS components. Alternatively, PLS regression can be formulated as a least squares problem restricted to a Krylov subspace. This equivalent formulation is employed to analyze the distance between ${\hat{\boldsymbol\beta}\;}_{\mathrm{PLS}}^{\scriptscriptstyle {(L)}}$, the PLS estimator of the vector of coefficients of the linear regression model based on $L$ PLS components, and $\hat{\boldsymbol \beta}_{\mathrm{OLS}}$, the one obtained by ordinary least squares (OLS), as a function of $L$. Specifically, ${\hat{\boldsymbol\beta}\;}_{\mathrm{PLS}}^{\scriptscriptstyle {(L)}}$ is the vector of coefficients in the aforementioned Krylov subspace that is closest to $\hat{\boldsymbol \beta}_{\mathrm{OLS}}$ in terms of the Mahalanobis distance with respect to the covariance matrix of the OLS estimate. We provide a bound on this distance that depends only on the distribution of the eigenvalues of the regressor covariance matrix. Numerical examples on synthetic and real-world data are used to illustrate how the distance between ${\hat{\boldsymbol\beta}\;}_{\mathrm{PLS}}^{\scriptscriptstyle {(L)}}$ and $\hat{\boldsymbol \beta}_{\mathrm{OLS}}$ depends on the number of clusters in which the eigenvalues of the regressor covariance matrix are grouped.

scikit-fda: A Python Package for Functional Data Analysis

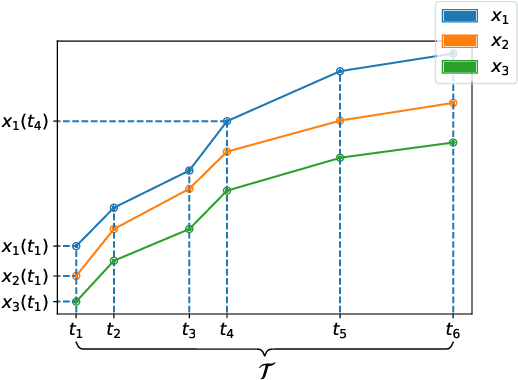
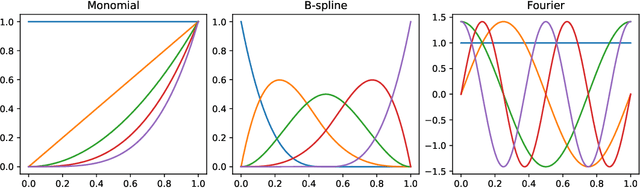
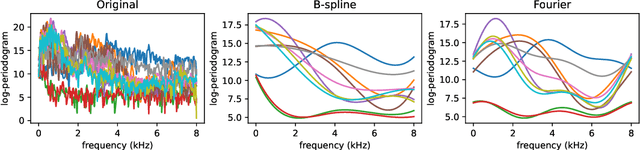
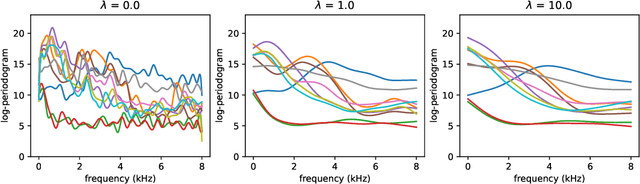
The library scikit-fda is a Python package for Functional Data Analysis (FDA). It provides a comprehensive set of tools for representation, preprocessing, and exploratory analysis of functional data. The library is built upon and integrated in Python's scientific ecosystem. In particular, it conforms to the scikit-learn application programming interface so as to take advantage of the functionality for machine learning provided by this package: pipelines, model selection, and hyperparameter tuning, among others. The scikit-fda package has been released as free and open-source software under a 3-Clause BSD license and is open to contributions from the FDA community. The library's extensive documentation includes step-by-step tutorials and detailed examples of use.

Feature selection in functional data classification with recursive maxima hunting

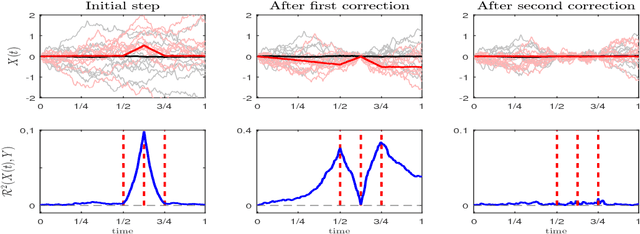
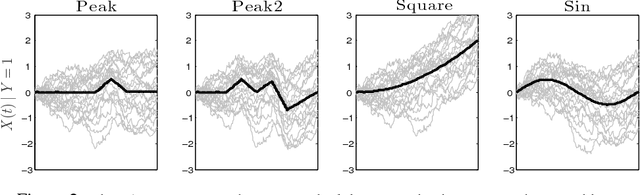
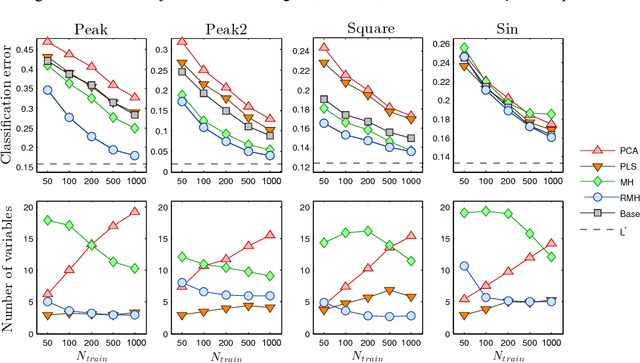
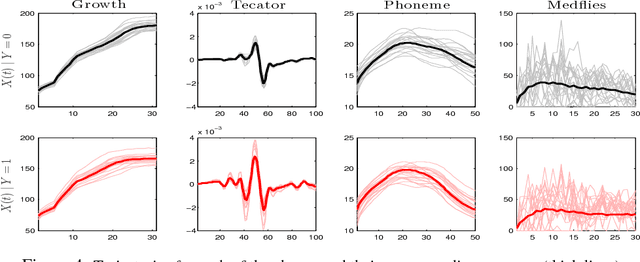
Dimensionality reduction is one of the key issues in the design of effective machine learning methods for automatic induction. In this work, we introduce recursive maxima hunting (RMH) for variable selection in classification problems with functional data. In this context, variable selection techniques are especially attractive because they reduce the dimensionality, facilitate the interpretation and can improve the accuracy of the predictive models. The method, which is a recursive extension of maxima hunting (MH), performs variable selection by identifying the maxima of a relevance function, which measures the strength of the correlation of the predictor functional variable with the class label. At each stage, the information associated with the selected variable is removed by subtracting the conditional expectation of the process. The results of an extensive empirical evaluation are used to illustrate that, in the problems investigated, RMH has comparable or higher predictive accuracy than the standard dimensionality reduction techniques, such as PCA and PLS, and state-of-the-art feature selection methods for functional data, such as maxima hunting.

Pooling homogeneous ensembles to build heterogeneous ensembles

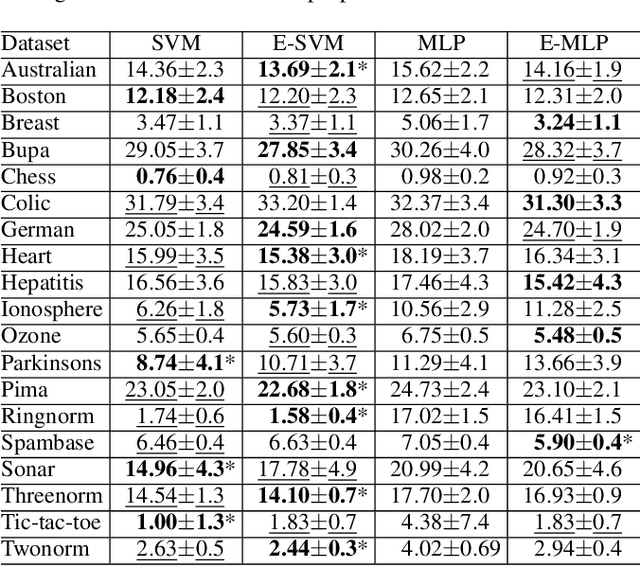
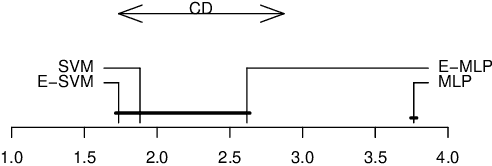
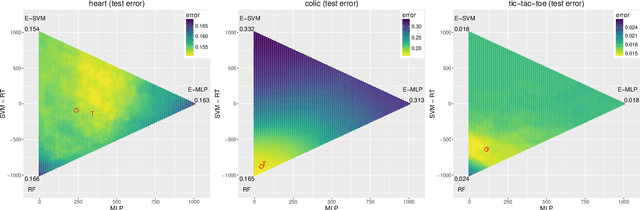
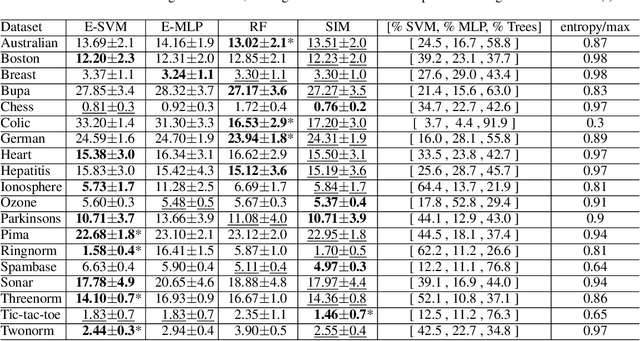
In ensemble methods, the outputs of a collection of diverse classifiers are combined in the expectation that the global prediction be more accurate than the individual ones. Heterogeneous ensembles consist of predictors of different types, which are likely to have different biases. If these biases are complementary, the combination of their decisions is beneficial. In this work, a family of heterogeneous ensembles is built by pooling classifiers from M homogeneous ensembles of different types of size T. Depending on the fraction of base classifiers of each type, a particular heterogeneous combination in this family is represented by a point in a regular simplex in M dimensions. The M vertices of this simplex represent the different homogeneous ensembles. A displacement away from one of these vertices effects a smooth transformation of the corresponding homogeneous ensemble into a heterogeneous one. The optimal composition of such heterogeneous ensemble can be determined using cross-validation or, if bootstrap samples are used to build the individual classifiers, out-of-bag data. An empirical analysis of such combinations of bootstraped ensembles composed of neural networks, SVMs, and random trees (i.e. from a standard random forest) illustrates the gains that can be achieved by this heterogeneous ensemble creation method.

Vote-boosting ensembles

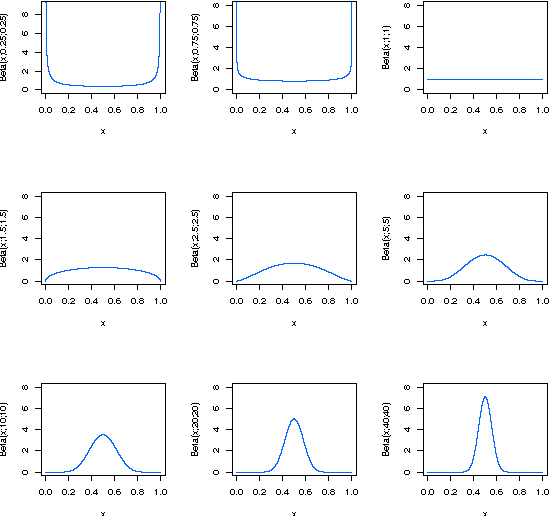
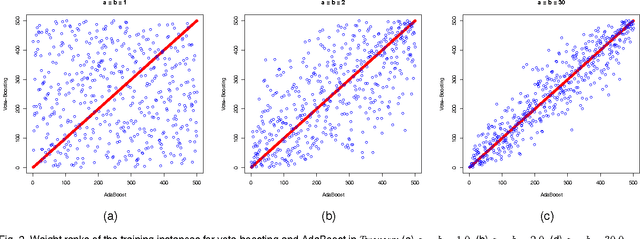
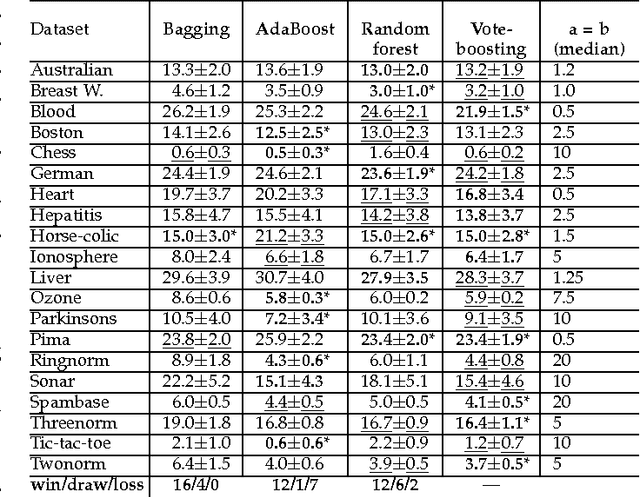
Vote-boosting is a sequential ensemble learning method in which the individual classifiers are built on different weighted versions of the training data. To build a new classifier, the weight of each training instance is determined in terms of the degree of disagreement among the current ensemble predictions for that instance. For low class-label noise levels, especially when simple base learners are used, emphasis should be made on instances for which the disagreement rate is high. When more flexible classifiers are used and as the noise level increases, the emphasis on these uncertain instances should be reduced. In fact, at sufficiently high levels of class-label noise, the focus should be on instances on which the ensemble classifiers agree. The optimal type of emphasis can be automatically determined using cross-validation. An extensive empirical analysis using the beta distribution as emphasis function illustrates that vote-boosting is an effective method to generate ensembles that are both accurate and robust.

Non-linear Causal Inference using Gaussianity Measures

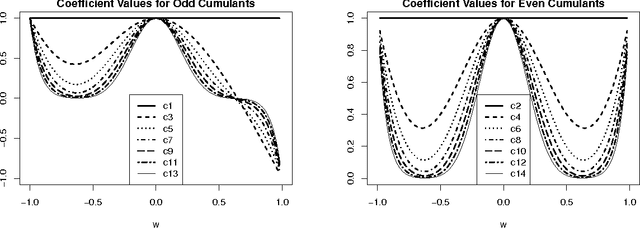
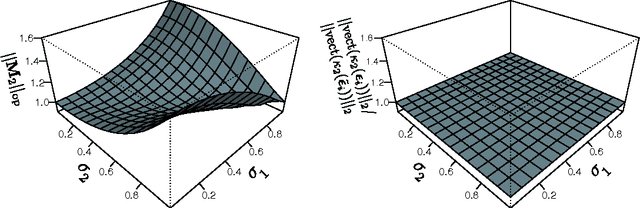
We provide theoretical and empirical evidence for a type of asymmetry between causes and effects that is present when these are related via linear models contaminated with additive non-Gaussian noise. Assuming that the causes and the effects have the same distribution, we show that the distribution of the residuals of a linear fit in the anti-causal direction is closer to a Gaussian than the distribution of the residuals in the causal direction. This Gaussianization effect is characterized by reduction of the magnitude of the high-order cumulants and by an increment of the differential entropy of the residuals. The problem of non-linear causal inference is addressed by performing an embedding in an expanded feature space, in which the relation between causes and effects can be assumed to be linear. The effectiveness of a method to discriminate between causes and effects based on this type of asymmetry is illustrated in a variety of experiments using different measures of Gaussianity. The proposed method is shown to be competitive with state-of-the-art techniques for causal inference.