Pooling homogeneous ensembles to build heterogeneous ensembles

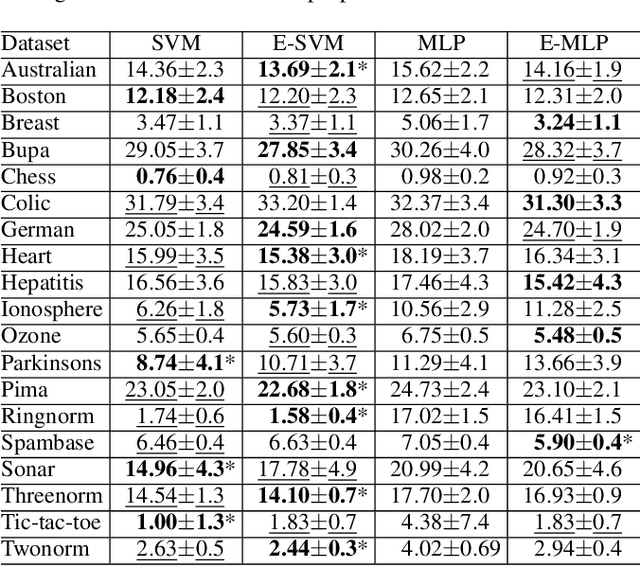
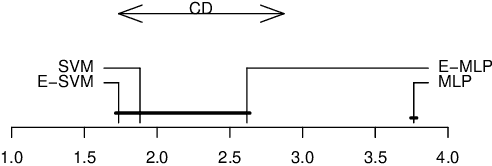
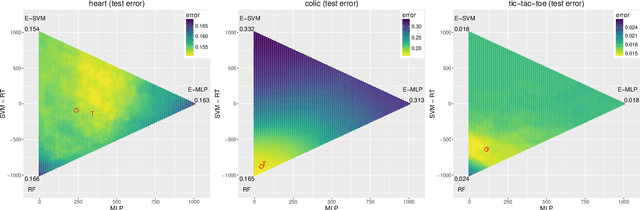
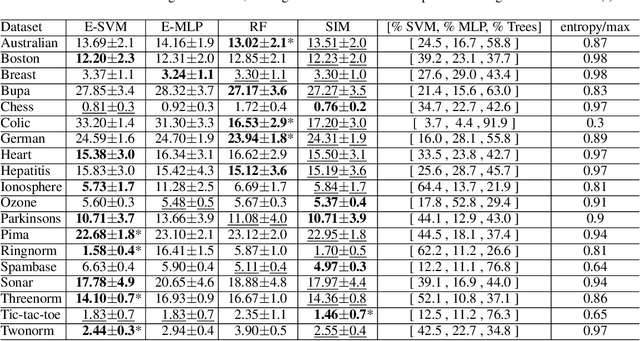
In ensemble methods, the outputs of a collection of diverse classifiers are combined in the expectation that the global prediction be more accurate than the individual ones. Heterogeneous ensembles consist of predictors of different types, which are likely to have different biases. If these biases are complementary, the combination of their decisions is beneficial. In this work, a family of heterogeneous ensembles is built by pooling classifiers from M homogeneous ensembles of different types of size T. Depending on the fraction of base classifiers of each type, a particular heterogeneous combination in this family is represented by a point in a regular simplex in M dimensions. The M vertices of this simplex represent the different homogeneous ensembles. A displacement away from one of these vertices effects a smooth transformation of the corresponding homogeneous ensemble into a heterogeneous one. The optimal composition of such heterogeneous ensemble can be determined using cross-validation or, if bootstrap samples are used to build the individual classifiers, out-of-bag data. An empirical analysis of such combinations of bootstraped ensembles composed of neural networks, SVMs, and random trees (i.e. from a standard random forest) illustrates the gains that can be achieved by this heterogeneous ensemble creation method.