Amparo Baillo
Supervised functional classification: A theoretical remark and some comparisons
Jun 17, 2008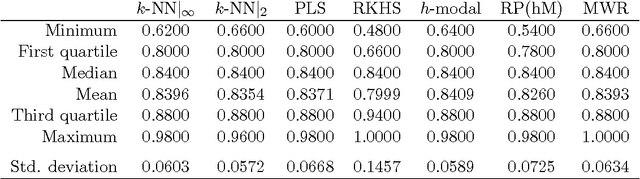
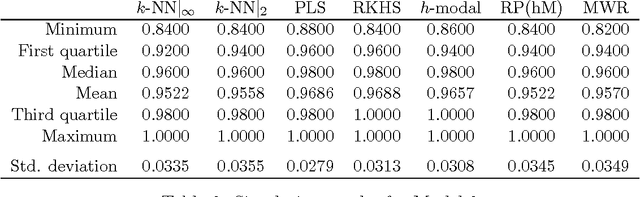
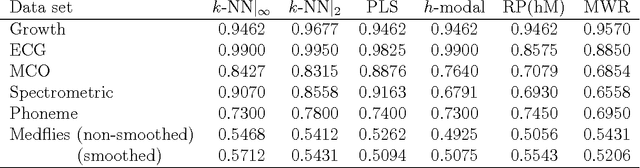
Abstract:The problem of supervised classification (or discrimination) with functional data is considered, with a special interest on the popular k-nearest neighbors (k-NN) classifier. First, relying on a recent result by Cerou and Guyader (2006), we prove the consistency of the k-NN classifier for functional data whose distribution belongs to a broad family of Gaussian processes with triangular covariance functions. Second, on a more practical side, we check the behavior of the k-NN method when compared with a few other functional classifiers. This is carried out through a small simulation study and the analysis of several real functional data sets. While no global "uniform" winner emerges from such comparisons, the overall performance of the k-NN method, together with its sound intuitive motivation and relative simplicity, suggests that it could represent a reasonable benchmark for the classification problem with functional data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge