On consistent estimation of dimension values

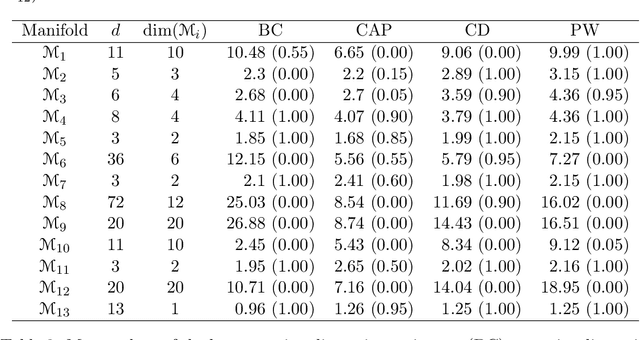
The problem of estimating, from a random sample of points, the dimension of a compact subset S of the Euclidean space is considered. The emphasis is put on consistency results in the statistical sense. That is, statements of convergence to the true dimension value when the sample size grows to infinity. Among the many available definitions of dimension, we have focused (on the grounds of its statistical tractability) on three notions: the Minkowski dimension, the correlation dimension and the, perhaps less popular, concept of pointwise dimension. We prove the statistical consistency of some natural estimators of these quantities. Our proofs partially rely on the use of an instrumental estimator formulated in terms of the empirical volume function Vn (r), defined as the Lebesgue measure of the set of points whose distance to the sample is at most r. In particular, we explore the case in which the true volume function V (r) of the target set S is a polynomial on some interval starting at zero. An empirical study is also included. Our study aims to provide some theoretical support, and some practical insights, for the problem of deciding whether or not the set S has a dimension smaller than that of the ambient space. This is a major statistical motivation of the dimension studies, in connection with the so-called Manifold Hypothesis.

Learning for Spatial Branching: An Algorithm Selection Approach

The use of machine learning techniques to improve the performance of branch-and-bound optimization algorithms is a very active area in the context of mixed integer linear problems, but little has been done for non-linear optimization. To bridge this gap, we develop a learning framework for spatial branching and show its efficacy in the context of the Reformulation-Linearization Technique for polynomial optimization problems. The proposed learning is performed offline, based on instance-specific features and with no computational overhead when solving new instances. Novel graph-based features are introduced, which turn out to play an important role for the learning. Experiments on different benchmark instances from the literature show that the learning-based branching rule significantly outperforms the standard rules.