Bissan Ghaddar
Joint Matching and Pricing for Crowd-shipping with In-store Customers
Jul 02, 2025Abstract:This paper examines the use of in-store customers as delivery couriers in a centralized crowd-shipping system, targeting the growing need for efficient last-mile delivery in urban areas. We consider a brick-and-mortar retail setting where shoppers are offered compensation to deliver time-sensitive online orders. To manage this process, we propose a Markov Decision Process (MDP) model that captures key uncertainties, including the stochastic arrival of orders and crowd-shippers, and the probabilistic acceptance of delivery offers. Our solution approach integrates Neural Approximate Dynamic Programming (NeurADP) for adaptive order-to-shopper assignment with a Deep Double Q-Network (DDQN) for dynamic pricing. This joint optimization strategy enables multi-drop routing and accounts for offer acceptance uncertainty, aligning more closely with real-world operations. Experimental results demonstrate that the integrated NeurADP + DDQN policy achieves notable improvements in delivery cost efficiency, with up to 6.7\% savings over NeurADP with fixed pricing and approximately 18\% over myopic baselines. We also show that allowing flexible delivery delays and enabling multi-destination routing further reduces operational costs by 8\% and 17\%, respectively. These findings underscore the advantages of dynamic, forward-looking policies in crowd-shipping systems and offer practical guidance for urban logistics operators.
Artificial Intelligence for Operations Research: Revolutionizing the Operations Research Process
Jan 06, 2024
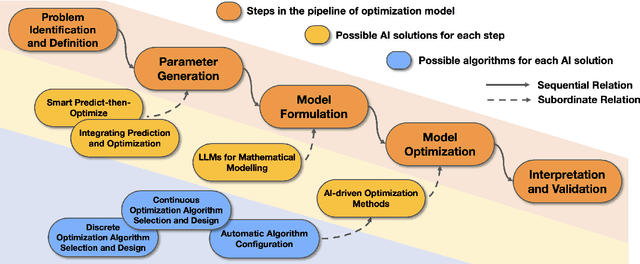
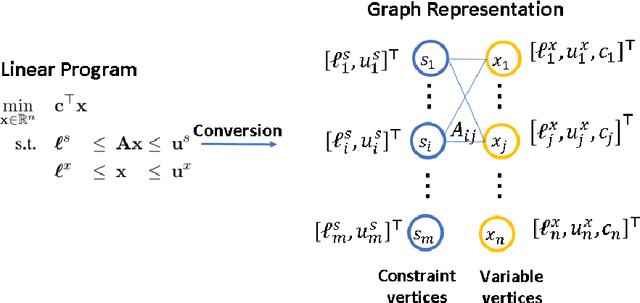
Abstract:The rapid advancement of artificial intelligence (AI) techniques has opened up new opportunities to revolutionize various fields, including operations research (OR). This survey paper explores the integration of AI within the OR process (AI4OR) to enhance its effectiveness and efficiency across multiple stages, such as parameter generation, model formulation, and model optimization. By providing a comprehensive overview of the state-of-the-art and examining the potential of AI to transform OR, this paper aims to inspire further research and innovation in the development of AI-enhanced OR methods and tools. The synergy between AI and OR is poised to drive significant advancements and novel solutions in a multitude of domains, ultimately leading to more effective and efficient decision-making.
NL4Opt Competition: Formulating Optimization Problems Based on Their Natural Language Descriptions
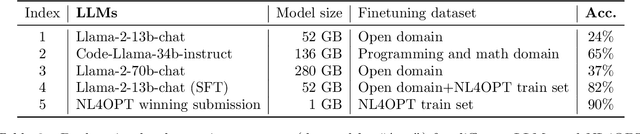
Mar 27, 2023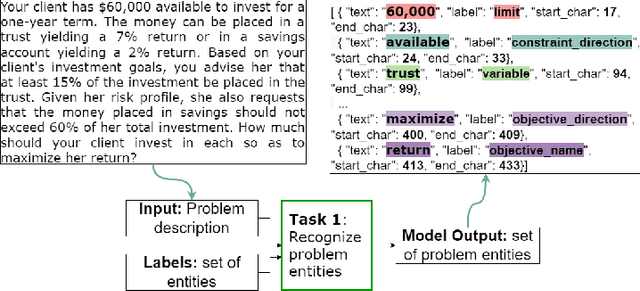

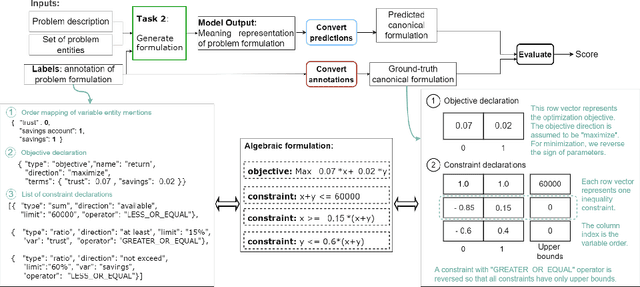
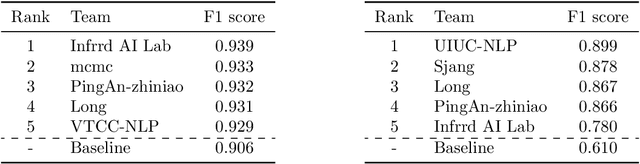
Abstract:The Natural Language for Optimization (NL4Opt) Competition was created to investigate methods of extracting the meaning and formulation of an optimization problem based on its text description. Specifically, the goal of the competition is to increase the accessibility and usability of optimization solvers by allowing non-experts to interface with them using natural language. We separate this challenging goal into two sub-tasks: (1) recognize and label the semantic entities that correspond to the components of the optimization problem; (2) generate a meaning representation (i.e., a logical form) of the problem from its detected problem entities. The first task aims to reduce ambiguity by detecting and tagging the entities of the optimization problems. The second task creates an intermediate representation of the linear programming (LP) problem that is converted into a format that can be used by commercial solvers. In this report, we present the LP word problem dataset and shared tasks for the NeurIPS 2022 competition. Furthermore, we investigate and compare the performance of the ChatGPT large language model against the winning solutions. Through this competition, we hope to bring interest towards the development of novel machine learning applications and datasets for optimization modeling.
Polynomial Optimization: Enhancing RLT relaxations with Conic Constraints
Aug 11, 2022



Abstract:Conic optimization has recently emerged as a powerful tool for designing tractable and guaranteed algorithms for non-convex polynomial optimization problems. On the one hand, tractability is crucial for efficiently solving large-scale problems and, on the other hand, strong bounds are needed to ensure high quality solutions. In this research, we investigate the strengthening of RLT relaxations of polynomial optimization problems through the addition of nine different types of constraints that are based on linear, second-order cone, and semidefinite programming to solve to optimality the instances of well established test sets of polynomial optimization problems. We describe how to design these conic constraints and their performance with respect to each other and with respect to the standard RLT relaxations. Our first finding is that the different variants of nonlinear constraints (second-order cone and semidefinite) are the best performing ones in around $50\%$ of the instances. Additionally, we present a machine learning approach to decide on the most suitable constraints to add for a given instance. The computational results show that the machine learning approach significantly outperforms each and every one of the nine individual approaches.
Learning for Spatial Branching: An Algorithm Selection Approach
Apr 22, 2022



Abstract:The use of machine learning techniques to improve the performance of branch-and-bound optimization algorithms is a very active area in the context of mixed integer linear problems, but little has been done for non-linear optimization. To bridge this gap, we develop a learning framework for spatial branching and show its efficacy in the context of the Reformulation-Linearization Technique for polynomial optimization problems. The proposed learning is performed offline, based on instance-specific features and with no computational overhead when solving new instances. Novel graph-based features are introduced, which turn out to play an important role for the learning. Experiments on different benchmark instances from the literature show that the learning-based branching rule significantly outperforms the standard rules.
Deep Reinforcement Learning for Electric Vehicle Routing Problem with Time Windows
Oct 05, 2020
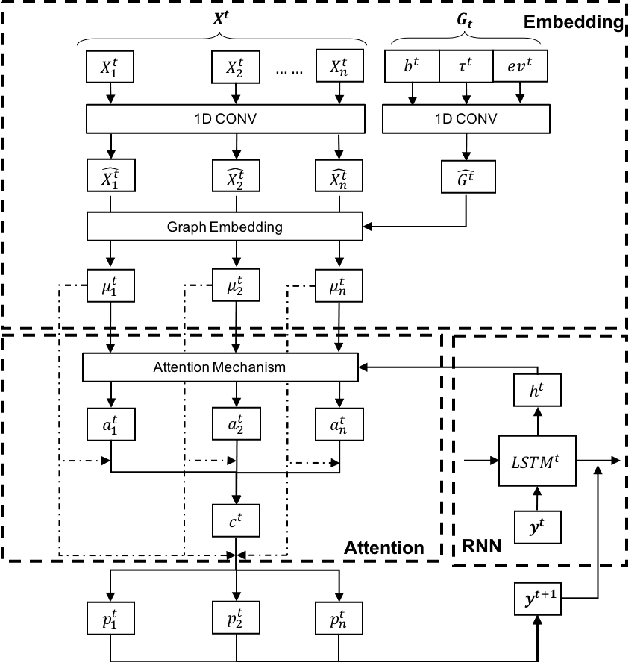
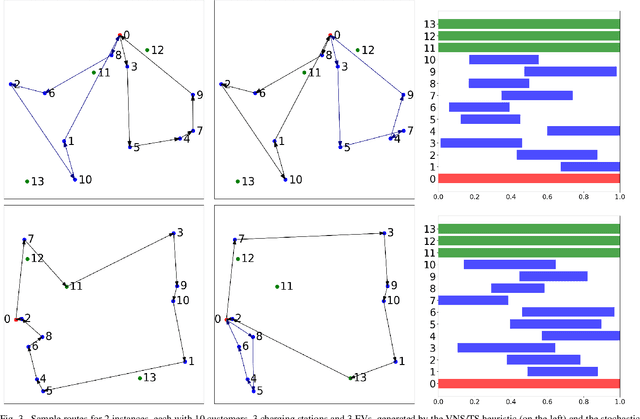
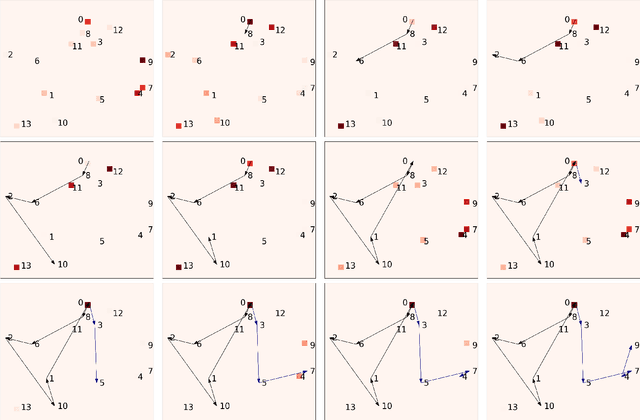
Abstract:The past decade has seen a rapid penetration of electric vehicles (EV) in the market, more and more logistics and transportation companies start to deploy EVs for service provision. In order to model the operations of a commercial EV fleet, we utilize the EV routing problem with time windows (EVRPTW). In this research, we propose an end-to-end deep reinforcement learning framework to solve the EVRPTW. In particular, we develop an attention model incorporating the pointer network and a graph embedding technique to parameterize a stochastic policy for solving the EVRPTW. The model is then trained using policy gradient with rollout baseline. Our numerical studies show that the proposed model is able to efficiently solve EVRPTW instances of large sizes that are not solvable with any existing approaches.
Optimization Models for Machine Learning: A Survey
Jan 21, 2019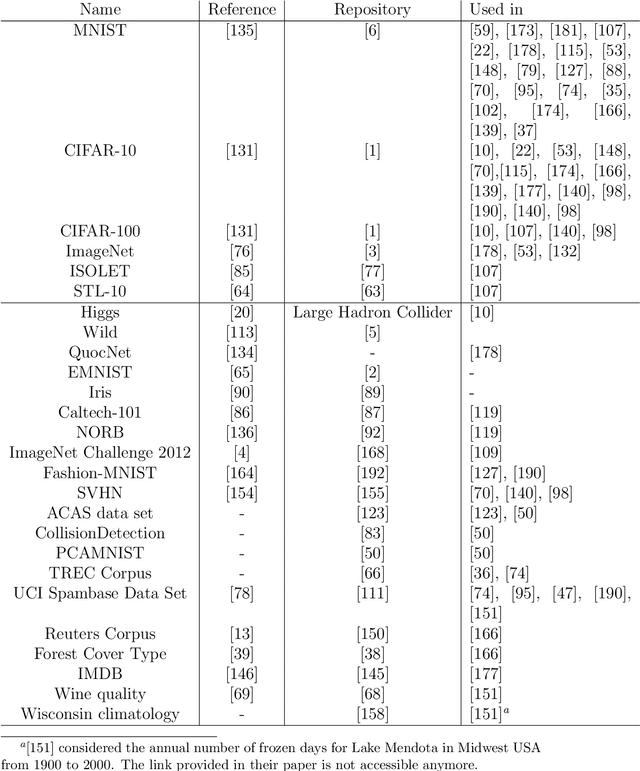
Abstract:This paper surveys the machine learning literature and presents machine learning as optimization models. Such models can benefit from the advancement of numerical optimization techniques which have already played a distinctive role in several machine learning settings. Particularly, mathematical optimization models are presented for commonly used machine learning approaches for regression, classification, clustering, and deep neural networks as well new emerging applications in machine teaching and empirical model learning. The strengths and the shortcomings of these models are discussed and potential research directions are highlighted.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge