GROS: A General Robust Aggregation Strategy

A new, very general, robust procedure for combining estimators in metric spaces is introduced GROS. The method is reminiscent of the well-known median of means, as described in \cite{devroye2016sub}. Initially, the sample is divided into $K$ groups. Subsequently, an estimator is computed for each group. Finally, these $K$ estimators are combined using a robust procedure. We prove that this estimator is sub-Gaussian and we get its break-down point, in the sense of Donoho. The robust procedure involves a minimization problem on a general metric space, but we show that the same (up to a constant) sub-Gaussianity is obtained if the minimization is taken over the sample, making GROS feasible in practice. The performance of GROS is evaluated through five simulation studies: the first one focuses on classification using $k$-means, the second one on the multi-armed bandit problem, the third one on the regression problem. The fourth one is the set estimation problem under a noisy model. Lastly, we apply GROS to get a robust persistent diagram.

Regression with Missing Data, a Comparison Study of TechniquesBased on Random Forests

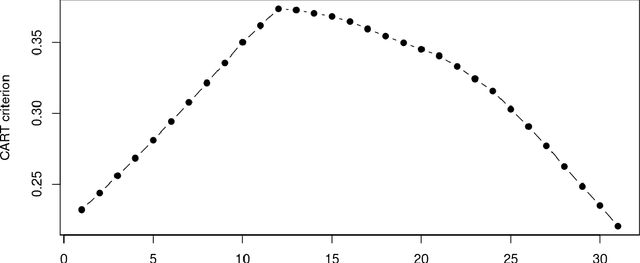
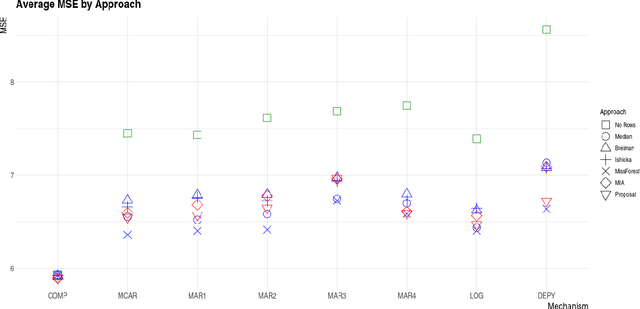
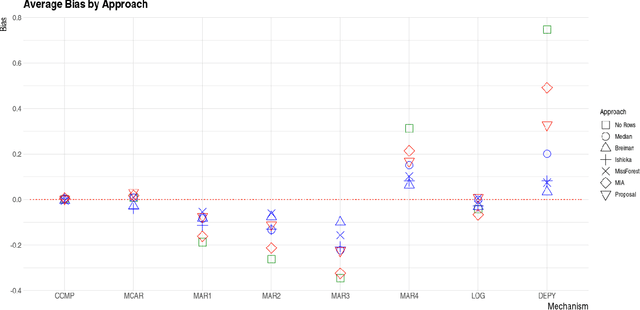
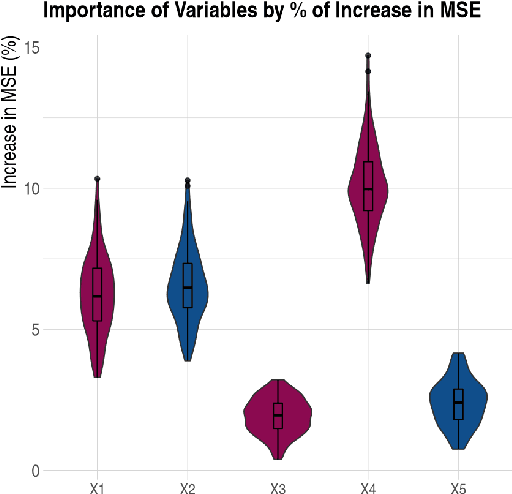
In this paper we present the practical benefits of a new random forest algorithm to deal withmissing values in the sample. The purpose of this work is to compare the different solutionsto deal with missing values with random forests and describe our new algorithm performanceas well as its algorithmic complexity. A variety of missing value mechanisms (such as MCAR,MAR, MNAR) are considered and simulated. We study the quadratic errors and the bias ofour algorithm and compare it to the most popular missing values random forests algorithms inthe literature. In particular, we compare those techniques for both a regression and predictionpurpose. This work follows a first paper Gomez-Mendez and Joly (2020) on the consistency ofthis new algorithm.