Reda Chhaibi
IMT
Feature Representation Transferring to Lightweight Models via Perception Coherence
May 10, 2025Abstract:In this paper, we propose a method for transferring feature representation to lightweight student models from larger teacher models. We mathematically define a new notion called \textit{perception coherence}. Based on this notion, we propose a loss function, which takes into account the dissimilarities between data points in feature space through their ranking. At a high level, by minimizing this loss function, the student model learns to mimic how the teacher model \textit{perceives} inputs. More precisely, our method is motivated by the fact that the representational capacity of the student model is weaker than the teacher model. Hence, we aim to develop a new method allowing for a better relaxation. This means that, the student model does not need to preserve the absolute geometry of the teacher one, while preserving global coherence through dissimilarity ranking. Our theoretical insights provide a probabilistic perspective on the process of feature representation transfer. Our experiments results show that our method outperforms or achieves on-par performance compared to strong baseline methods for representation transferring.
Convolutional Rectangular Attention Module
Mar 13, 2025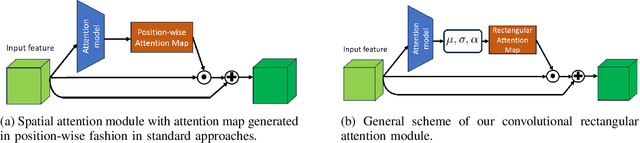
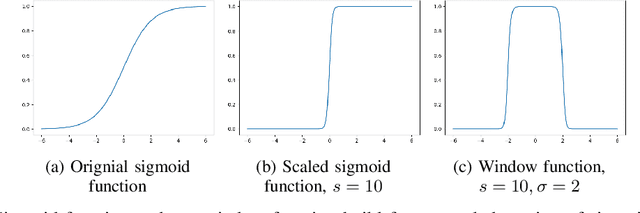
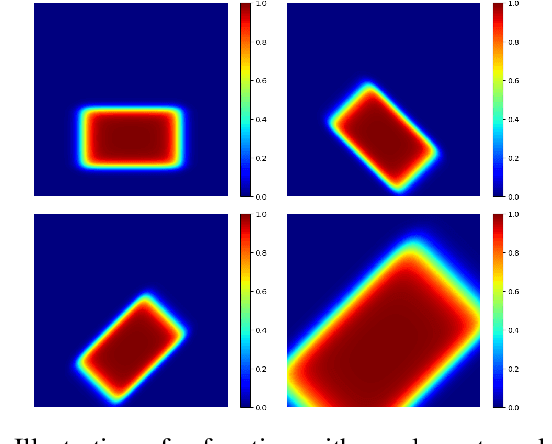
Abstract:In this paper, we introduce a novel spatial attention module, that can be integrated to any convolutional network. This module guides the model to pay attention to the most discriminative part of an image. This enables the model to attain a better performance by an end-to-end training. In standard approaches, a spatial attention map is generated in a position-wise fashion. We observe that this results in very irregular boundaries. This could make it difficult to generalize to new samples. In our method, the attention region is constrained to be rectangular. This rectangle is parametrized by only 5 parameters, allowing for a better stability and generalization to new samples. In our experiments, our method systematically outperforms the position-wise counterpart. Thus, this provides us a novel useful spatial attention mechanism for convolutional models. Besides, our module also provides the interpretability concerning the ``where to look" question, as it helps to know the part of the input on which the model focuses to produce the prediction.
Large Margin Discriminative Loss for Classification
May 28, 2024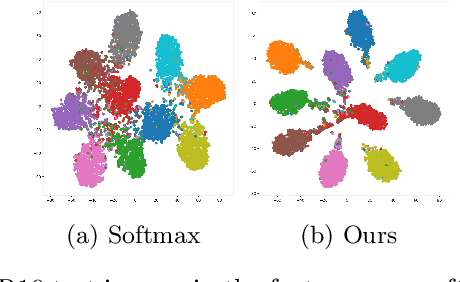
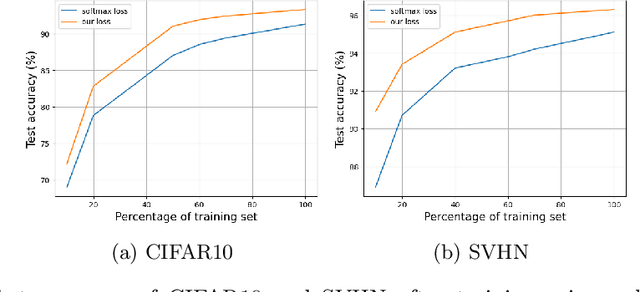
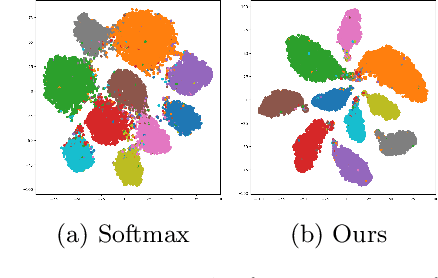
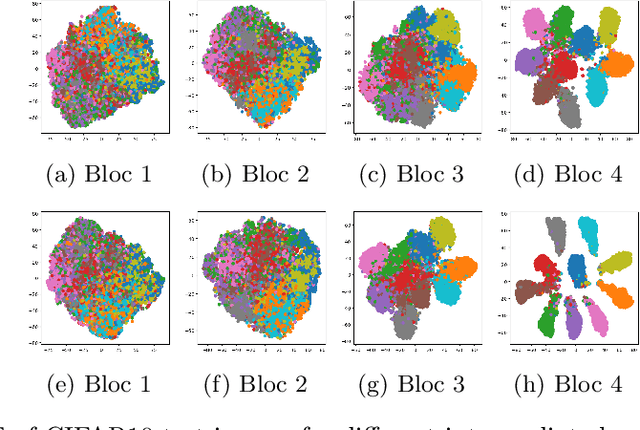
Abstract:In this paper, we introduce a novel discriminative loss function with large margin in the context of Deep Learning. This loss boosts the discriminative power of neural nets, represented by intra-class compactness and inter-class separability. On the one hand, the class compactness is ensured by close distance of samples of the same class to each other. On the other hand, the inter-class separability is boosted by a margin loss that ensures the minimum distance of each class to its closest boundary. All the terms in our loss have an explicit meaning, giving a direct view of the feature space obtained. We analyze mathematically the relation between compactness and margin term, giving a guideline about the impact of the hyper-parameters on the learned features. Moreover, we also analyze properties of the gradient of the loss with respect to the parameters of the neural net. Based on this, we design a strategy called partial momentum updating that enjoys simultaneously stability and consistency in training. Furthermore, we also investigate generalization errors to have better theoretical insights. Our loss function systematically boosts the test accuracy of models compared to the standard softmax loss in our experiments.
Sensitivity Analysis for Active Sampling, with Applications to the Simulation of Analog Circuits
May 13, 2024



Abstract:We propose an active sampling flow, with the use-case of simulating the impact of combined variations on analog circuits. In such a context, given the large number of parameters, it is difficult to fit a surrogate model and to efficiently explore the space of design features. By combining a drastic dimension reduction using sensitivity analysis and Bayesian surrogate modeling, we obtain a flexible active sampling flow. On synthetic and real datasets, this flow outperforms the usual Monte-Carlo sampling which often forms the foundation of design space exploration.
Statistical Edge Detection And UDF Learning For Shape Representation
May 06, 2024Abstract:In the field of computer vision, the numerical encoding of 3D surfaces is crucial. It is classical to represent surfaces with their Signed Distance Functions (SDFs) or Unsigned Distance Functions (UDFs). For tasks like representation learning, surface classification, or surface reconstruction, this function can be learned by a neural network, called Neural Distance Function. This network, and in particular its weights, may serve as a parametric and implicit representation for the surface. The network must represent the surface as accurately as possible. In this paper, we propose a method for learning UDFs that improves the fidelity of the obtained Neural UDF to the original 3D surface. The key idea of our method is to concentrate the learning effort of the Neural UDF on surface edges. More precisely, we show that sampling more training points around surface edges allows better local accuracy of the trained Neural UDF, and thus improves the global expressiveness of the Neural UDF in terms of Hausdorff distance. To detect surface edges, we propose a new statistical method based on the calculation of a $p$-value at each point on the surface. Our method is shown to detect surface edges more accurately than a commonly used local geometric descriptor.
Combining Statistical Depth and Fermat Distance for Uncertainty Quantification
Apr 12, 2024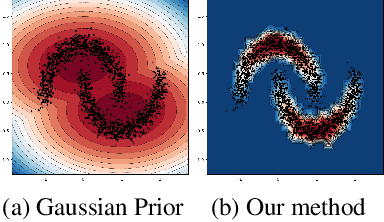
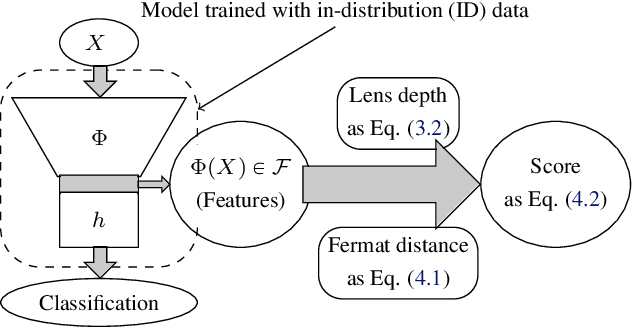
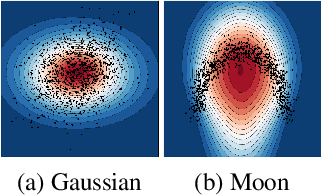
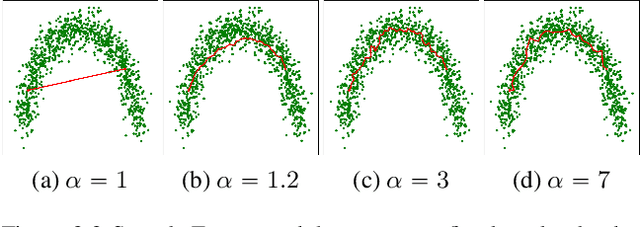
Abstract:We measure the Out-of-domain uncertainty in the prediction of Neural Networks using a statistical notion called ``Lens Depth'' (LD) combined with Fermat Distance, which is able to capture precisely the ``depth'' of a point with respect to a distribution in feature space, without any assumption about the form of distribution. Our method has no trainable parameter. The method is applicable to any classification model as it is applied directly in feature space at test time and does not intervene in training process. As such, it does not impact the performance of the original model. The proposed method gives excellent qualitative result on toy datasets and can give competitive or better uncertainty estimation on standard deep learning datasets compared to strong baseline methods.
Free Probability, Newton lilypads and Jacobians of neural networks
Nov 01, 2021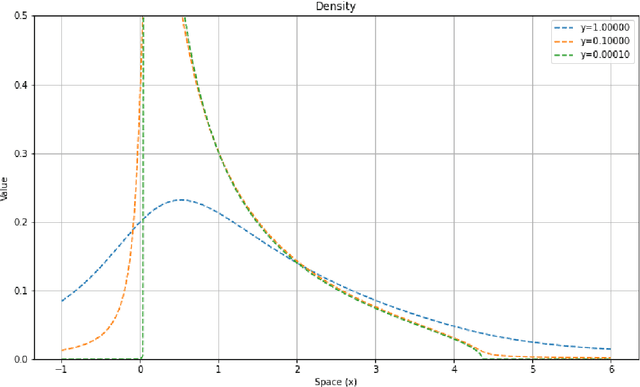

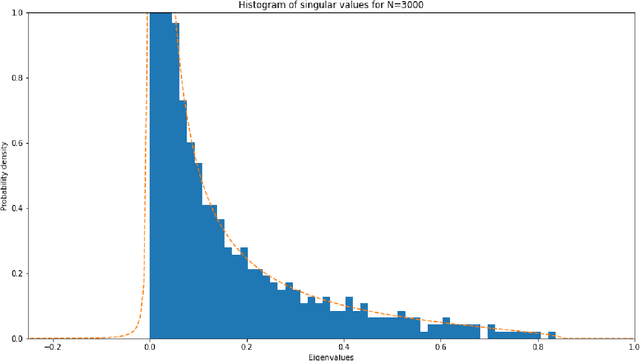
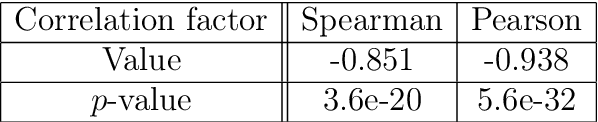
Abstract:Gradient descent during the learning process of a neural network can be subject to many instabilities. The spectral density of the Jacobian is a key component for analyzing robustness. Following the works of Pennington et al., such Jacobians are modeled using free multiplicative convolutions from Free Probability Theory. We present a reliable and very fast method for computing the associated spectral densities. This method has a controlled and proven convergence. Our technique is based on an adaptative Newton-Raphson scheme, by finding and chaining basins of attraction: the Newton algorithm finds contiguous lilypad-like basins and steps from one to the next, heading towards the objective. We demonstrate the applicability of our method by using it to assess how the learning process is affected by network depth, layer widths and initialization choices: empirically, final test losses are very correlated to our Free Probability metrics.
Geodesics in fibered latent spaces: A geometric approach to learning correspondences between conditions
May 24, 2020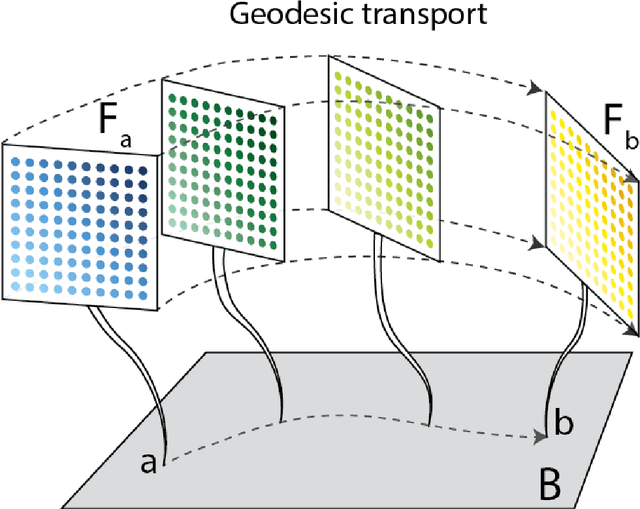
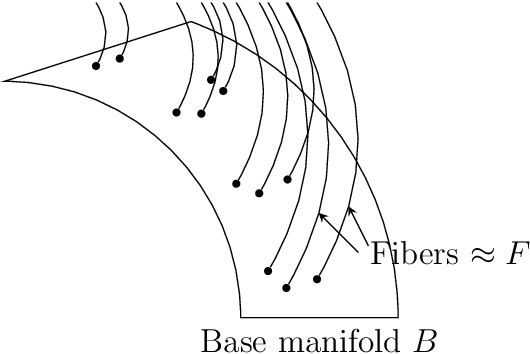
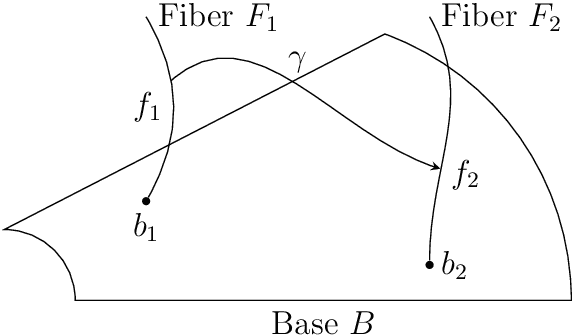
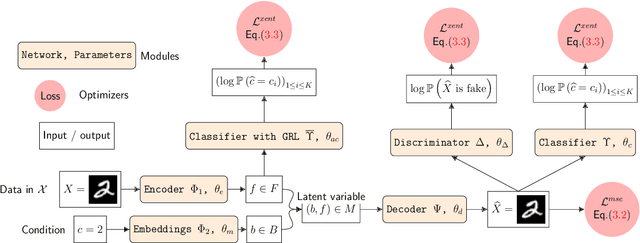
Abstract:This work introduces a geometric framework and a novel network architecture for creating correspondences between samples of different conditions. Under this formalism, the latent space is a fiber bundle stratified into a base space encoding conditions, and a fiber space encoding the variations within conditions. The correspondences between conditions are obtained by minimizing an energy functional, resulting in diffeomorphism flows between fibers. We illustrate this approach using MNIST and Olivetti and benchmark its performances on the task of batch correction, which is the problem of integrating multiple biological datasets together.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge