Free Probability, Newton lilypads and Jacobians of neural networks

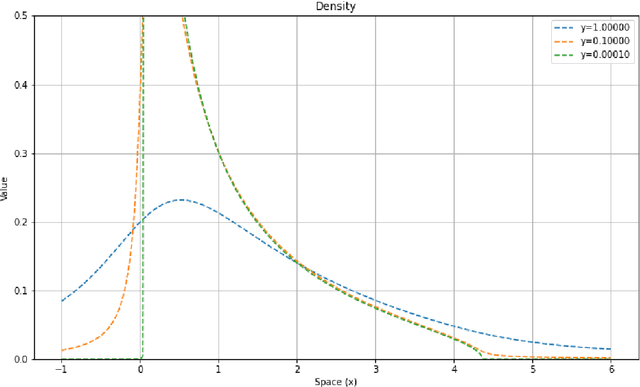
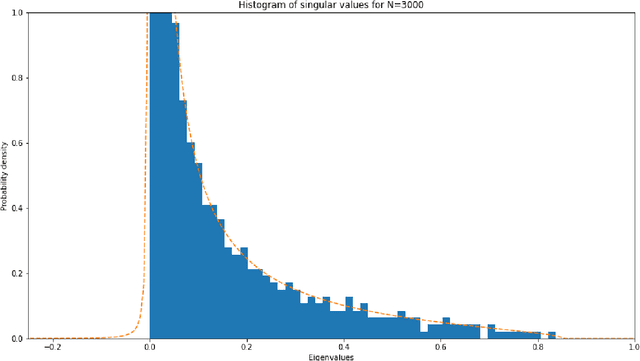
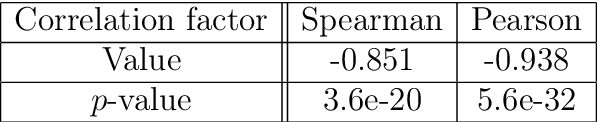
Gradient descent during the learning process of a neural network can be subject to many instabilities. The spectral density of the Jacobian is a key component for analyzing robustness. Following the works of Pennington et al., such Jacobians are modeled using free multiplicative convolutions from Free Probability Theory. We present a reliable and very fast method for computing the associated spectral densities. This method has a controlled and proven convergence. Our technique is based on an adaptative Newton-Raphson scheme, by finding and chaining basins of attraction: the Newton algorithm finds contiguous lilypad-like basins and steps from one to the next, heading towards the objective. We demonstrate the applicability of our method by using it to assess how the learning process is affected by network depth, layer widths and initialization choices: empirically, final test losses are very correlated to our Free Probability metrics.

Geodesics in fibered latent spaces: A geometric approach to learning correspondences between conditions

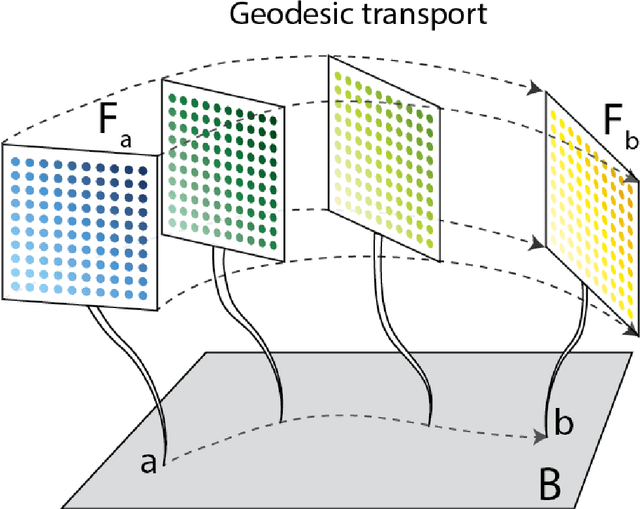
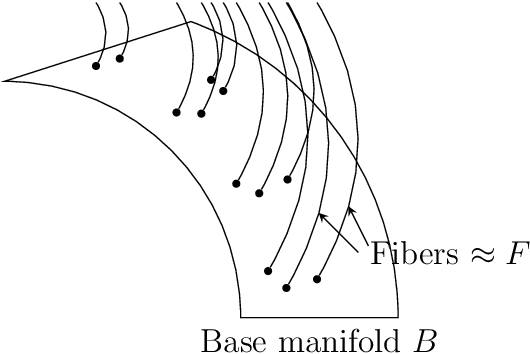
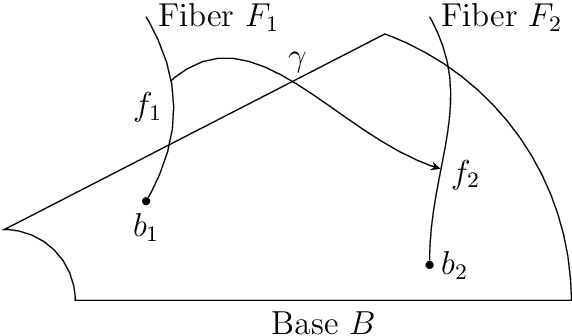
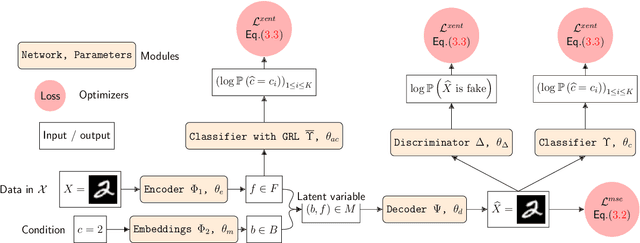
This work introduces a geometric framework and a novel network architecture for creating correspondences between samples of different conditions. Under this formalism, the latent space is a fiber bundle stratified into a base space encoding conditions, and a fiber space encoding the variations within conditions. The correspondences between conditions are obtained by minimizing an energy functional, resulting in diffeomorphism flows between fibers. We illustrate this approach using MNIST and Olivetti and benchmark its performances on the task of batch correction, which is the problem of integrating multiple biological datasets together.

Holographic Neural Architectures

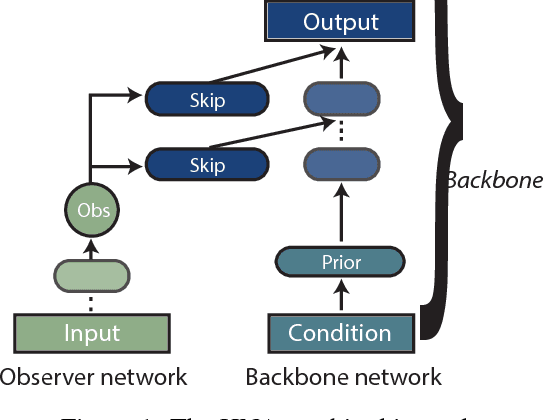
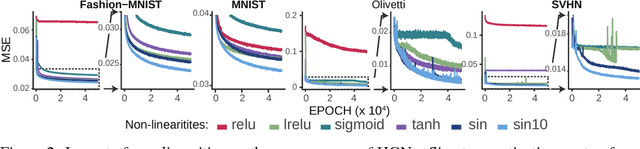
Representation learning is at the heart of what makes deep learning effective. In this work, we introduce a new framework for representation learning that we call "Holographic Neural Architectures" (HNAs). In the same way that an observer can experience the 3D structure of a holographed object by looking at its hologram from several angles, HNAs derive Holographic Representations from the training set. These representations can then be explored by moving along a continuous bounded single dimension. We show that HNAs can be used to make generative networks, state-of-the-art regression models and that they are inherently highly resistant to noise. Finally, we argue that because of their denoising abilities and their capacity to generalize well from very few examples, models based upon HNAs are particularly well suited for biological applications where training examples are rare or noisy.