Free Probability, Newton lilypads and Jacobians of neural networks

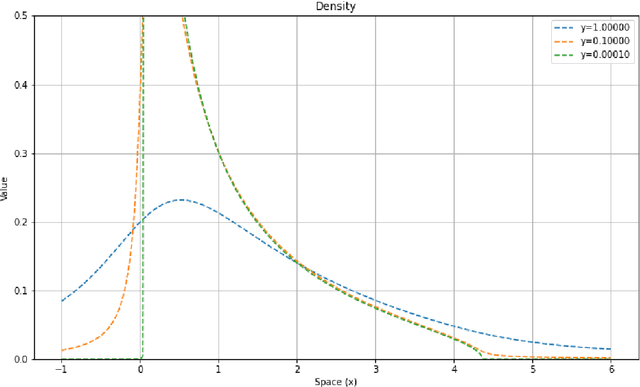
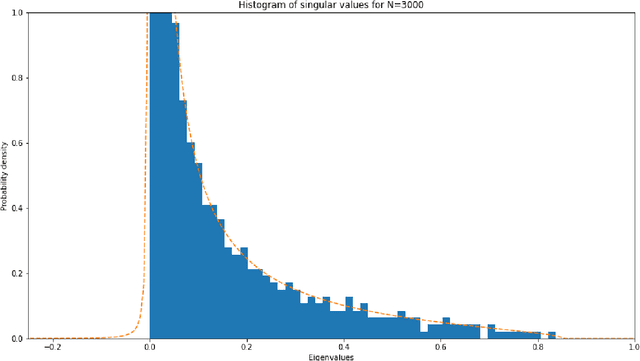
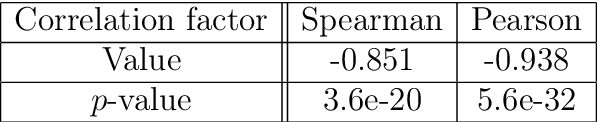
Gradient descent during the learning process of a neural network can be subject to many instabilities. The spectral density of the Jacobian is a key component for analyzing robustness. Following the works of Pennington et al., such Jacobians are modeled using free multiplicative convolutions from Free Probability Theory. We present a reliable and very fast method for computing the associated spectral densities. This method has a controlled and proven convergence. Our technique is based on an adaptative Newton-Raphson scheme, by finding and chaining basins of attraction: the Newton algorithm finds contiguous lilypad-like basins and steps from one to the next, heading towards the objective. We demonstrate the applicability of our method by using it to assess how the learning process is affected by network depth, layer widths and initialization choices: empirically, final test losses are very correlated to our Free Probability metrics.