Two-level deep domain decomposition method

This study presents a two-level Deep Domain Decomposition Method (Deep-DDM) augmented with a coarse-level network for solving boundary value problems using physics-informed neural networks (PINNs). The addition of the coarse level network improves scalability and convergence rates compared to the single level method. Tested on a Poisson equation with Dirichlet boundary conditions, the two-level deep DDM demonstrates superior performance, maintaining efficient convergence regardless of the number of subdomains. This advance provides a more scalable and effective approach to solving complex partial differential equations with machine learning.

A Block-Coordinate Approach of Multi-level Optimization with an Application to Physics-Informed Neural Networks

Multi-level methods are widely used for the solution of large-scale problems, because of their computational advantages and exploitation of the complementarity between the involved sub-problems. After a re-interpretation of multi-level methods from a block-coordinate point of view, we propose a multi-level algorithm for the solution of nonlinear optimization problems and analyze its evaluation complexity. We apply it to the solution of partial differential equations using physics-informed neural networks (PINNs) and show on a few test problems that the approach results in better solutions and significant computational savings

A coarse space acceleration of deep-DDM

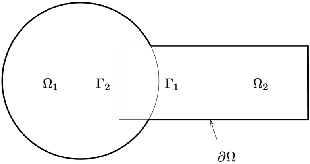
The use of deep learning methods for solving PDEs is a field in full expansion. In particular, Physical Informed Neural Networks, that implement a sampling of the physical domain and use a loss function that penalizes the violation of the partial differential equation, have shown their great potential. Yet, to address large scale problems encountered in real applications and compete with existing numerical methods for PDEs, it is important to design parallel algorithms with good scalability properties. In the vein of traditional domain decomposition methods (DDM), we consider the recently proposed deep-ddm approach. We present an extension of this method that relies on the use of a coarse space correction, similarly to what is done in traditional DDM solvers. Our investigations shows that the coarse correction is able to alleviate the deterioration of the convergence of the solver when the number of subdomains is increased thanks to an instantaneous information exchange between subdomains at each iteration. Experimental results demonstrate that our approach induces a remarkable acceleration of the original deep-ddm method, at a reduced additional computational cost.