Path-metrics, pruning, and generalization

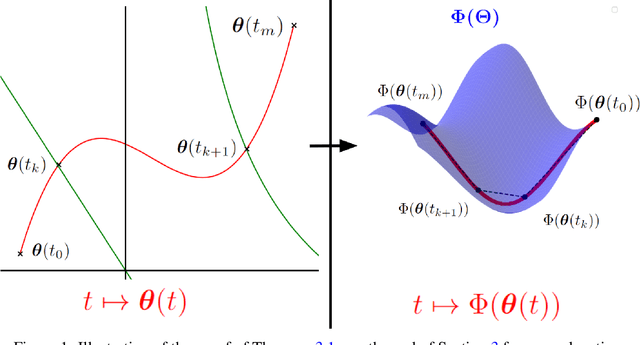
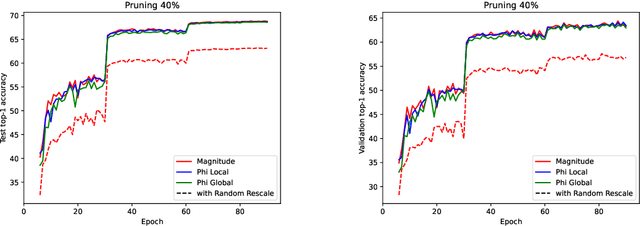
Analyzing the behavior of ReLU neural networks often hinges on understanding the relationships between their parameters and the functions they implement. This paper proves a new bound on function distances in terms of the so-called path-metrics of the parameters. Since this bound is intrinsically invariant with respect to the rescaling symmetries of the networks, it sharpens previously known bounds. It is also, to the best of our knowledge, the first bound of its kind that is broadly applicable to modern networks such as ResNets, VGGs, U-nets, and many more. In contexts such as network pruning and quantization, the proposed path-metrics can be efficiently computed using only two forward passes. Besides its intrinsic theoretical interest, the bound yields not only novel theoretical generalization bounds, but also a promising proof of concept for rescaling-invariant pruning.

A path-norm toolkit for modern networks: consequences, promises and challenges

This work introduces the first toolkit around path-norms that is fully able to encompass general DAG ReLU networks with biases, skip connections and any operation based on the extraction of order statistics: max pooling, GroupSort etc. This toolkit notably allows us to establish generalization bounds for modern neural networks that are not only the most widely applicable path-norm based ones, but also recover or beat the sharpest known bounds of this type. These extended path-norms further enjoy the usual benefits of path-norms: ease of computation, invariance under the symmetries of the network, and improved sharpness on feedforward networks compared to the product of operators' norms, another complexity measure most commonly used. The versatility of the toolkit and its ease of implementation allow us to challenge the concrete promises of path-norm-based generalization bounds, by numerically evaluating the sharpest known bounds for ResNets on ImageNet.

Approximation speed of quantized vs. unquantized ReLU neural networks and beyond

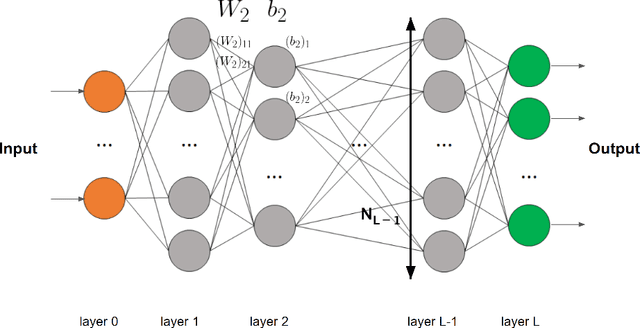
We consider general approximation families encompassing ReLU neural networks. On the one hand, we introduce a new property, that we call $\infty$-encodability, which lays a framework that we use (i) to guarantee that ReLU networks can be uniformly quantized and still have approximation speeds comparable to unquantized ones, and (ii) to prove that ReLU networks share a common limitation with many other approximation families: the approximation speed of a set C is bounded from above by an encoding complexity of C (a complexity well-known for many C's). The property of $\infty$-encodability allows us to unify and generalize known results in which it was implicitly used. On the other hand, we give lower and upper bounds on the Lipschitz constant of the mapping that associates the weights of a network to the function they represent in L^p. It is given in terms of the width, the depth of the network and a bound on the weight's norm, and it is based on well-known upper bounds on the Lipschitz constants of the functions represented by ReLU networks. This allows us to recover known results, to establish new bounds on covering numbers, and to characterize the accuracy of naive uniform quantization of ReLU networks.