Compressive Learning for Semi-Parametric Models
Paper and Code
Oct 22, 2019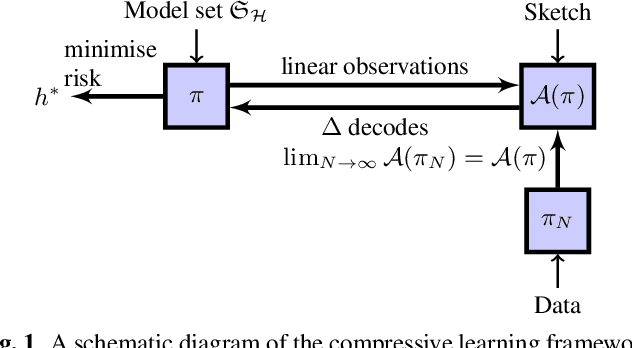
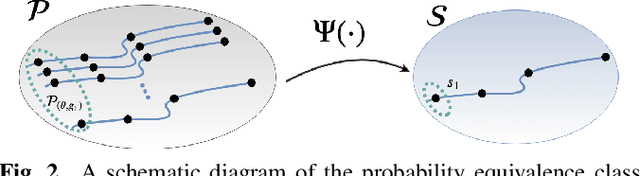
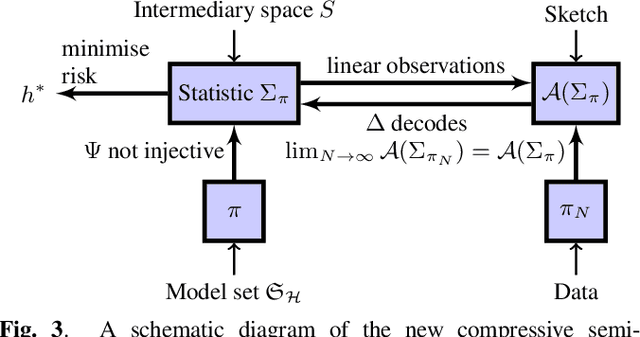
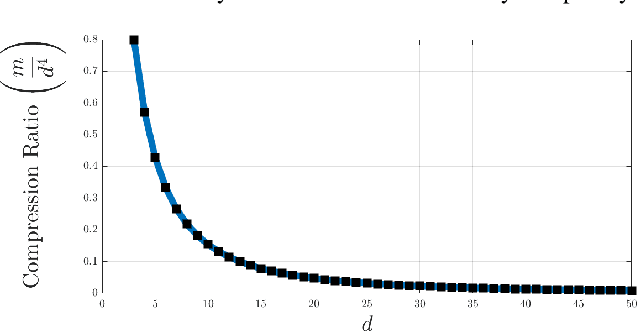
In the compressive learning theory, instead of solving a statistical learning problem from the input data, a so-called sketch is computed from the data prior to learning. The sketch has to capture enough information to solve the problem directly from it, allowing to discard the dataset from the memory. This is useful when dealing with large datasets as the size of the sketch does not scale with the size of the database. In this paper, we reformulate the original compressive learning framework to explicitly cater for the class of semi-parametric models. The reformulation takes account of the inherent topology and structure of semi-parametric models, creating an intuitive pathway to the development of compressive learning algorithms. We apply our developed framework to both the semi-parametric models of independent component analysis and subspace clustering, demonstrating the robustness of the framework to explicitly show when a compression in complexity can be achieved.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge