Sketched RT3D: How to reconstruct billions of photons per second

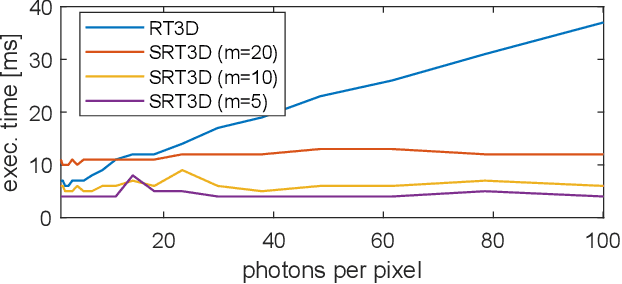
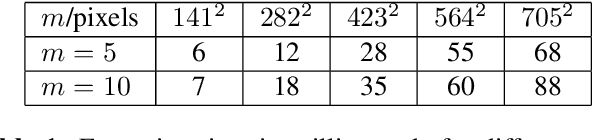
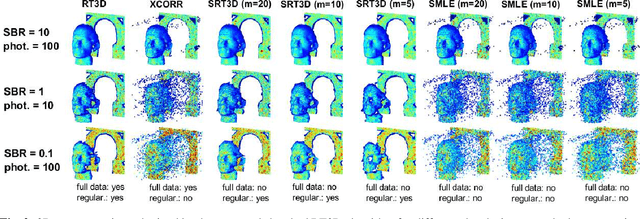
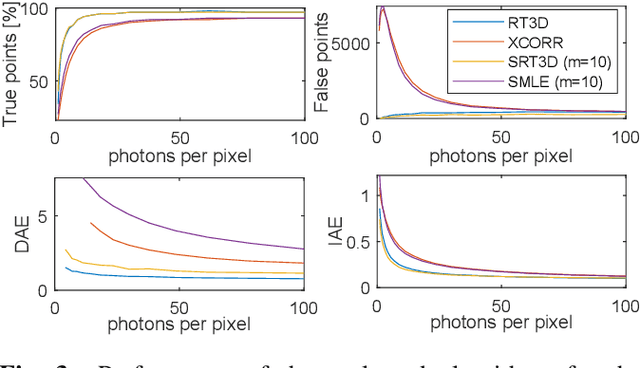
Single-photon light detection and ranging (lidar) captures depth and intensity information of a 3D scene. Reconstructing a scene from observed photons is a challenging task due to spurious detections associated with background illumination sources. To tackle this problem, there is a plethora of 3D reconstruction algorithms which exploit spatial regularity of natural scenes to provide stable reconstructions. However, most existing algorithms have computational and memory complexity proportional to the number of recorded photons. This complexity hinders their real-time deployment on modern lidar arrays which acquire billions of photons per second. Leveraging a recent lidar sketching framework, we show that it is possible to modify existing reconstruction algorithms such that they only require a small sketch of the photon information. In particular, we propose a sketched version of a recent state-of-the-art algorithm which uses point cloud denoisers to provide spatially regularized reconstructions. A series of experiments performed on real lidar datasets demonstrates a significant reduction of execution time and memory requirements, while achieving the same reconstruction performance than in the full data case.

Compressive Independent Component Analysis: Theory and Algorithms

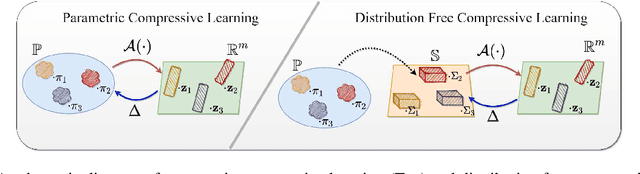
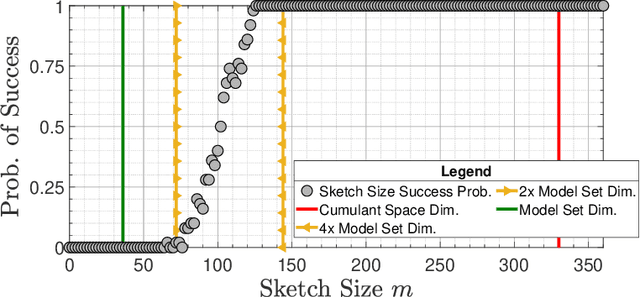
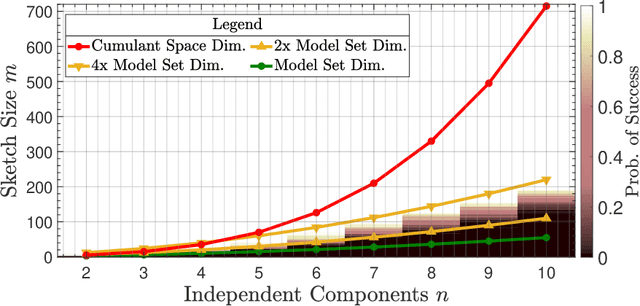
Compressive learning forms the exciting intersection between compressed sensing and statistical learning where one exploits forms of sparsity and structure to reduce the memory and/or computational complexity of the learning task. In this paper, we look at the independent component analysis (ICA) model through the compressive learning lens. In particular, we show that solutions to the cumulant based ICA model have particular structure that induces a low dimensional model set that resides in the cumulant tensor space. By showing a restricted isometry property holds for random cumulants e.g. Gaussian ensembles, we prove the existence of a compressive ICA scheme. Thereafter, we propose two algorithms of the form of an iterative projection gradient (IPG) and an alternating steepest descent (ASD) algorithm for compressive ICA, where the order of compression asserted from the restricted isometry property is realised through empirical results. We provide analysis of the CICA algorithms including the effects of finite samples. The effects of compression are characterised by a trade-off between the sketch size and the statistical efficiency of the ICA estimates. By considering synthetic and real datasets, we show the substantial memory gains achieved over well-known ICA algorithms by using one of the proposed CICA algorithms. Finally, we conclude the paper with open problems including interesting challenges from the emerging field of compressive learning.

Surface Detection for Sketched Single Photon Lidar

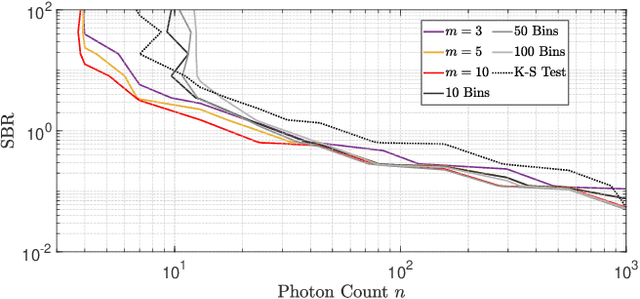
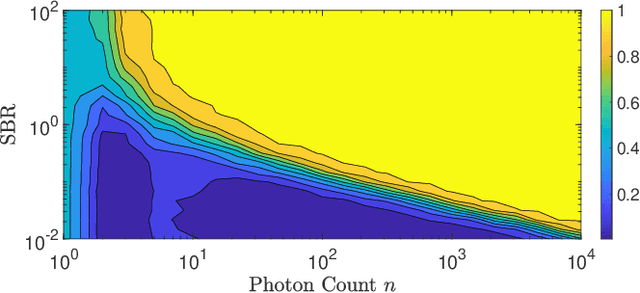
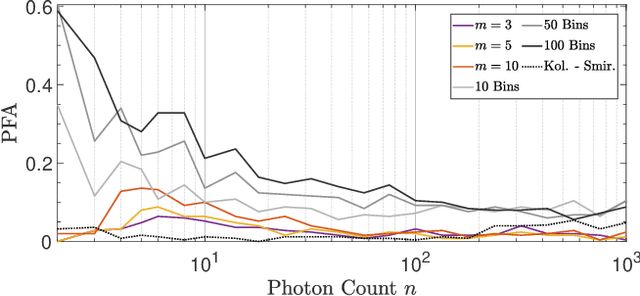
Single-photon lidar devices are able to collect an ever-increasing amount of time-stamped photons in small time periods due to increasingly larger arrays, generating a memory and computational bottleneck on the data processing side. Recently, a sketching technique was introduced to overcome this bottleneck which compresses the amount of information to be stored and processed. The size of the sketch scales with the number of underlying parameters of the time delay distribution and not, fundamentally, with either the number of detected photons or the time-stamp resolution. In this paper, we propose a detection algorithm based solely on a small sketch that determines if there are surfaces or objects in the scene or not. If a surface is detected, the depth and intensity of a single object can be computed in closed-form directly from the sketch. The computational load of the proposed detection algorithm depends solely on the size of the sketch, in contrast to previous algorithms that depend at least linearly in the number of collected photons or histogram bins, paving the way for fast, accurate and memory efficient lidar estimation. Our experiments demonstrate the memory and statistical efficiency of the proposed algorithm both on synthetic and real lidar datasets.

A Sketching Framework for Reduced Data Transfer in Photon Counting Lidar

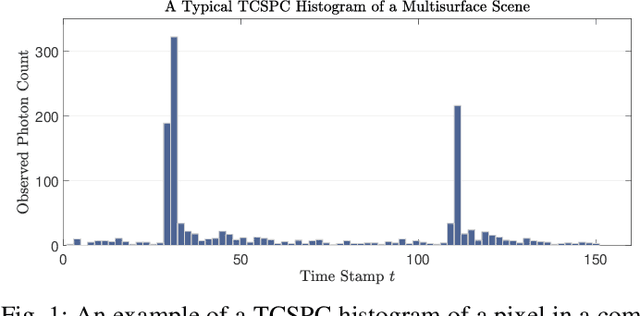
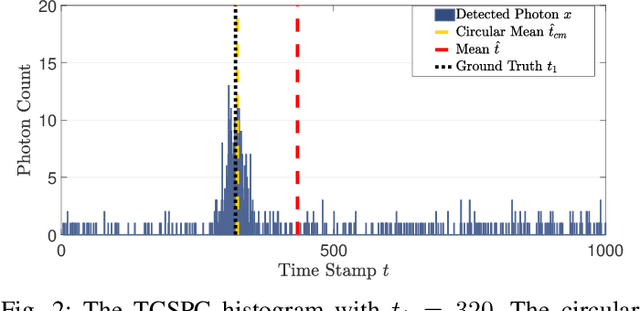
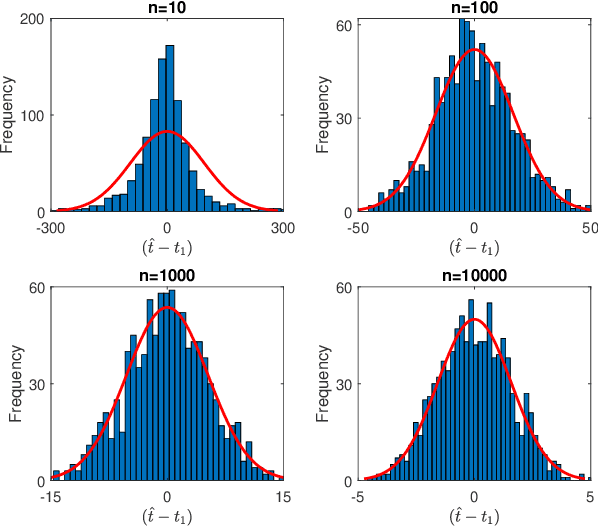
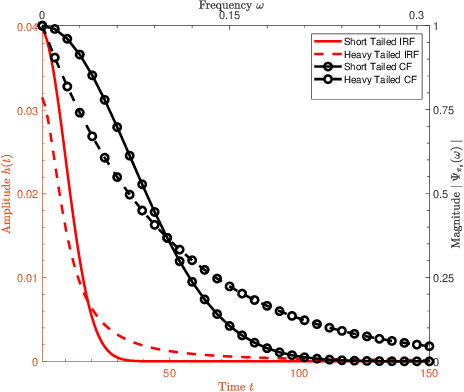
Single-photon lidar has become a prominent tool for depth imaging in recent years. At the core of the technique, the depth of a target is measured by constructing a histogram of time delays between emitted light pulses and detected photon arrivals. A major data processing bottleneck arises on the device when either the number of photons per pixel is large or the resolution of the time stamp is fine, as both the space requirement and the complexity of the image reconstruction algorithms scale with these parameters. We solve this limiting bottleneck of existing lidar techniques by sampling the characteristic function of the time of flight (ToF) model to build a compressive statistic, a so-called sketch of the time delay distribution, which is sufficient to infer the spatial distance and intensity of the object. The size of the sketch scales with the degrees of freedom of the ToF model (number of objects) and not, fundamentally, with the number of photons or the time stamp resolution. Moreover, the sketch is highly amenable for on-chip online processing. We show theoretically that the loss of information for compression is controlled and the mean squared error of the inference quickly converges towards the optimal Cram\'er-Rao bound (i.e. no loss of information) for modest sketch sizes. The proposed compressed single-photon lidar framework is tested and evaluated on real life datasets of complex scenes where it is shown that a compression rate of up-to 1/150 is achievable in practice without sacrificing the overall resolution of the reconstructed image.

Compressive Learning for Semi-Parametric Models

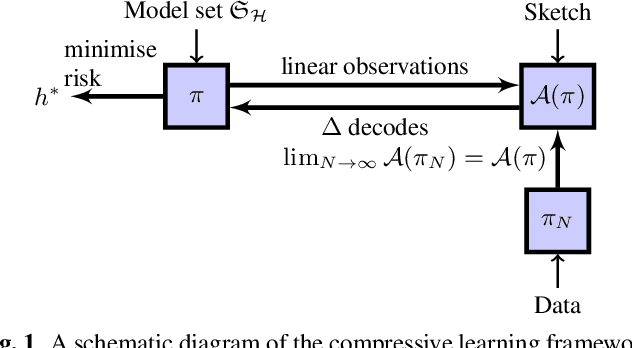
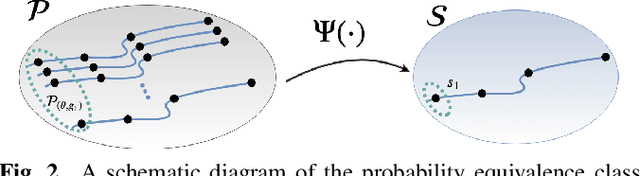
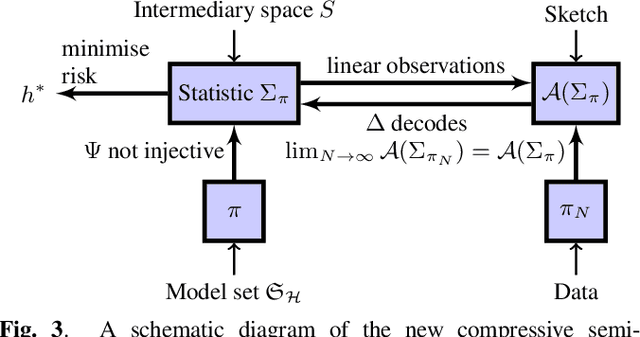
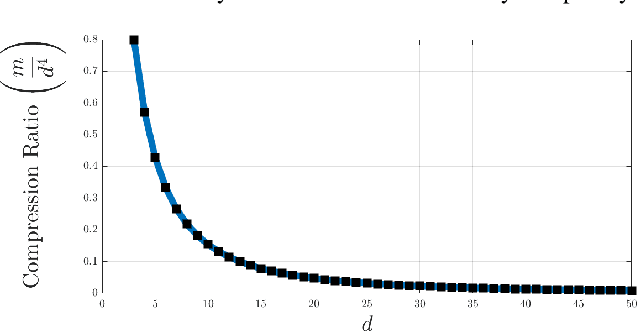
In the compressive learning theory, instead of solving a statistical learning problem from the input data, a so-called sketch is computed from the data prior to learning. The sketch has to capture enough information to solve the problem directly from it, allowing to discard the dataset from the memory. This is useful when dealing with large datasets as the size of the sketch does not scale with the size of the database. In this paper, we reformulate the original compressive learning framework to explicitly cater for the class of semi-parametric models. The reformulation takes account of the inherent topology and structure of semi-parametric models, creating an intuitive pathway to the development of compressive learning algorithms. We apply our developed framework to both the semi-parametric models of independent component analysis and subspace clustering, demonstrating the robustness of the framework to explicitly show when a compression in complexity can be achieved.