Compressive Independent Component Analysis: Theory and Algorithms
Paper and Code
Oct 15, 2021
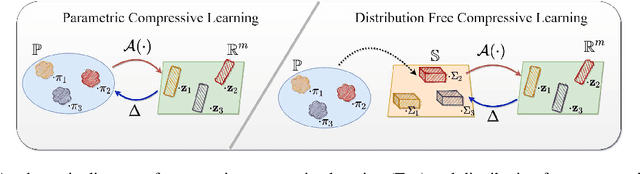
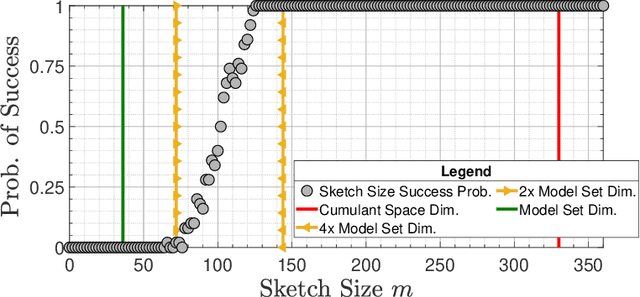
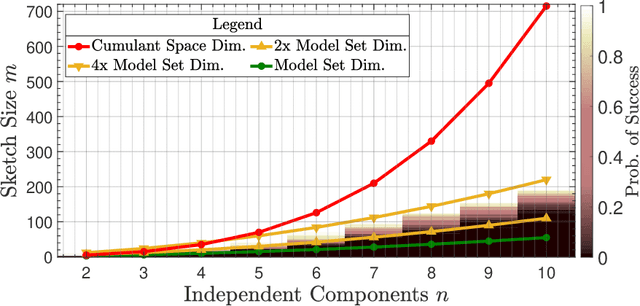
Compressive learning forms the exciting intersection between compressed sensing and statistical learning where one exploits forms of sparsity and structure to reduce the memory and/or computational complexity of the learning task. In this paper, we look at the independent component analysis (ICA) model through the compressive learning lens. In particular, we show that solutions to the cumulant based ICA model have particular structure that induces a low dimensional model set that resides in the cumulant tensor space. By showing a restricted isometry property holds for random cumulants e.g. Gaussian ensembles, we prove the existence of a compressive ICA scheme. Thereafter, we propose two algorithms of the form of an iterative projection gradient (IPG) and an alternating steepest descent (ASD) algorithm for compressive ICA, where the order of compression asserted from the restricted isometry property is realised through empirical results. We provide analysis of the CICA algorithms including the effects of finite samples. The effects of compression are characterised by a trade-off between the sketch size and the statistical efficiency of the ICA estimates. By considering synthetic and real datasets, we show the substantial memory gains achieved over well-known ICA algorithms by using one of the proposed CICA algorithms. Finally, we conclude the paper with open problems including interesting challenges from the emerging field of compressive learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge