Ensembles of Probabilistic Regression Trees

Tree-based ensemble methods such as random forests, gradient-boosted trees, and Bayesianadditive regression trees have been successfully used for regression problems in many applicationsand research studies. In this paper, we study ensemble versions of probabilisticregression trees that provide smooth approximations of the objective function by assigningeach observation to each region with respect to a probability distribution. We prove thatthe ensemble versions of probabilistic regression trees considered are consistent, and experimentallystudy their bias-variance trade-off and compare them with the state-of-the-art interms of performance prediction.

Knowledge Graph Completion via Complex Tensor Factorization

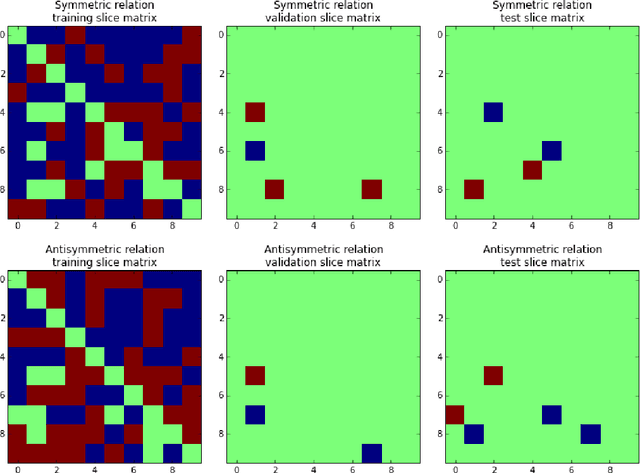
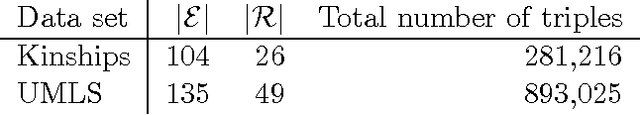
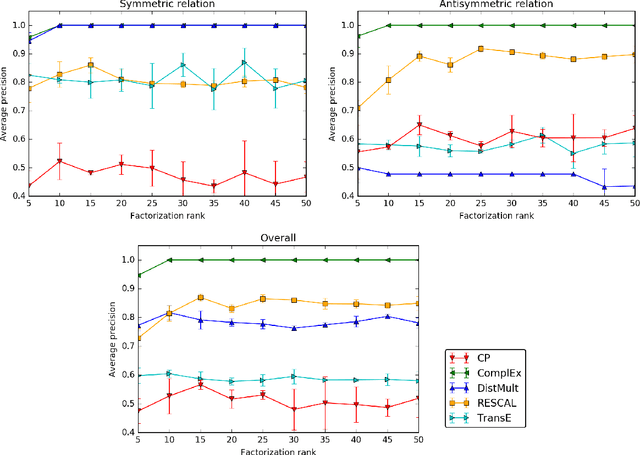
In statistical relational learning, knowledge graph completion deals with automatically understanding the structure of large knowledge graphs---labeled directed graphs---and predicting missing relationships---labeled edges. State-of-the-art embedding models propose different trade-offs between modeling expressiveness, and time and space complexity. We reconcile both expressiveness and complexity through the use of complex-valued embeddings and explore the link between such complex-valued embeddings and unitary diagonalization. We corroborate our approach theoretically and show that all real square matrices---thus all possible relation/adjacency matrices---are the real part of some unitarily diagonalizable matrix. This results opens the door to a lot of other applications of square matrices factorization. Our approach based on complex embeddings is arguably simple, as it only involves a Hermitian dot product, the complex counterpart of the standard dot product between real vectors, whereas other methods resort to more and more complicated composition functions to increase their expressiveness. The proposed complex embeddings are scalable to large data sets as it remains linear in both space and time, while consistently outperforming alternative approaches on standard link prediction benchmarks.

On Inductive Abilities of Latent Factor Models for Relational Learning

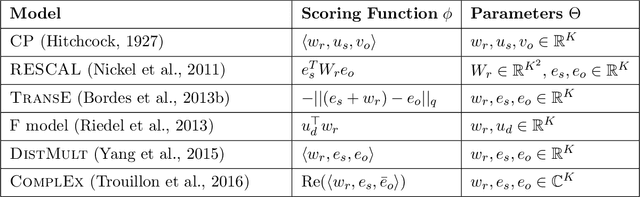
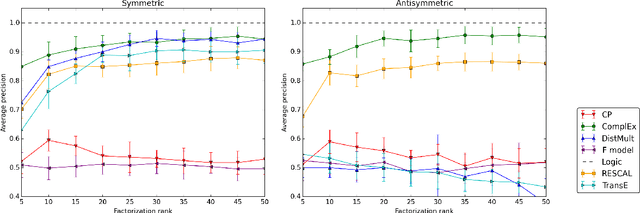
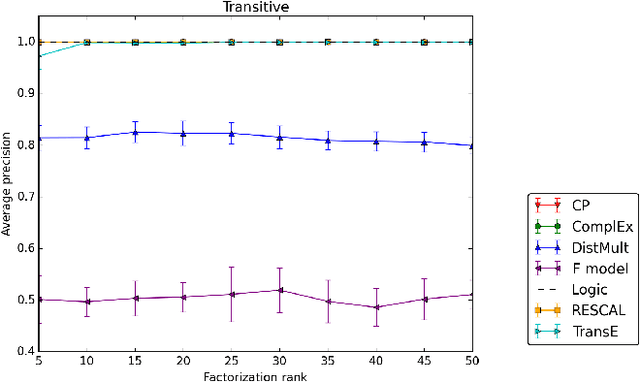
Latent factor models are increasingly popular for modeling multi-relational knowledge graphs. By their vectorial nature, it is not only hard to interpret why this class of models works so well, but also to understand where they fail and how they might be improved. We conduct an experimental survey of state-of-the-art models, not towards a purely comparative end, but as a means to get insight about their inductive abilities. To assess the strengths and weaknesses of each model, we create simple tasks that exhibit first, atomic properties of binary relations, and then, common inter-relational inference through synthetic genealogies. Based on these experimental results, we propose new research directions to improve on existing models.

Similarity Learning for Time Series Classification

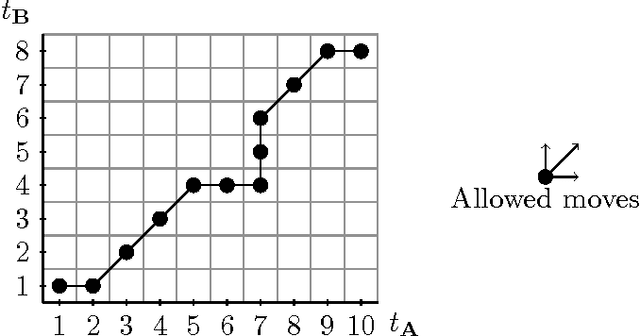
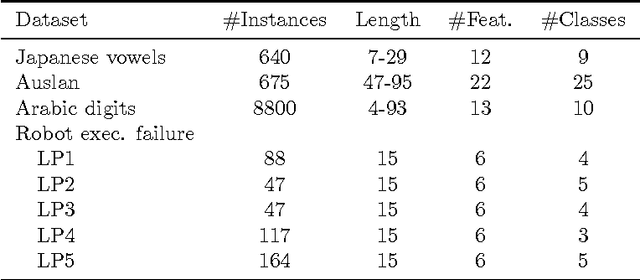
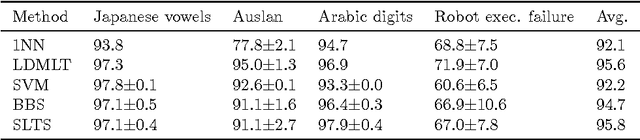
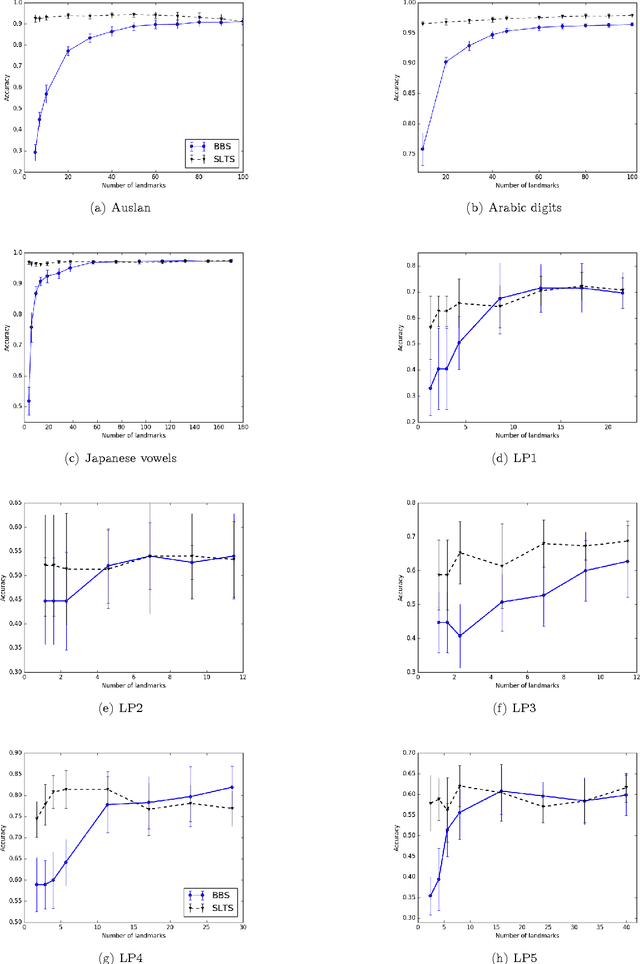
Multivariate time series naturally exist in many fields, like energy, bioinformatics, signal processing, and finance. Most of these applications need to be able to compare these structured data. In this context, dynamic time warping (DTW) is probably the most common comparison measure. However, not much research effort has been put into improving it by learning. In this paper, we propose a novel method for learning similarities based on DTW, in order to improve time series classification. Making use of the uniform stability framework, we provide the first theoretical guarantees in the form of a generalization bound for linear classification. The experimental study shows that the proposed approach is efficient, while yielding sparse classifiers.

Complex Embeddings for Simple Link Prediction

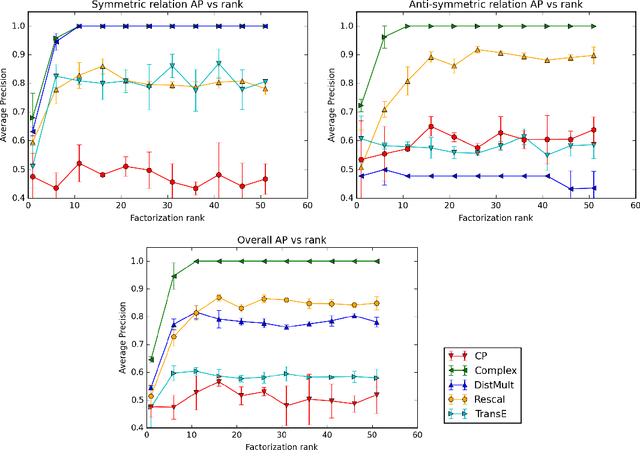
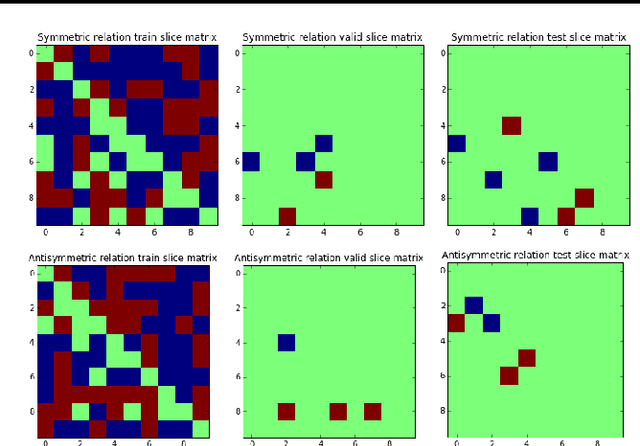
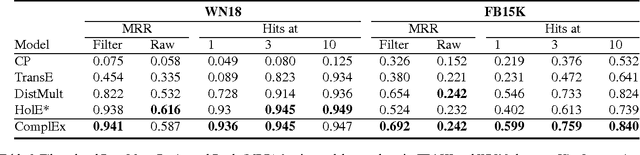
In statistical relational learning, the link prediction problem is key to automatically understand the structure of large knowledge bases. As in previous studies, we propose to solve this problem through latent factorization. However, here we make use of complex valued embeddings. The composition of complex embeddings can handle a large variety of binary relations, among them symmetric and antisymmetric relations. Compared to state-of-the-art models such as Neural Tensor Network and Holographic Embeddings, our approach based on complex embeddings is arguably simpler, as it only uses the Hermitian dot product, the complex counterpart of the standard dot product between real vectors. Our approach is scalable to large datasets as it remains linear in both space and time, while consistently outperforming alternative approaches on standard link prediction benchmarks.

Algorithmic Robustness for Learning via $(ε, γ, τ)$-Good Similarity Functions

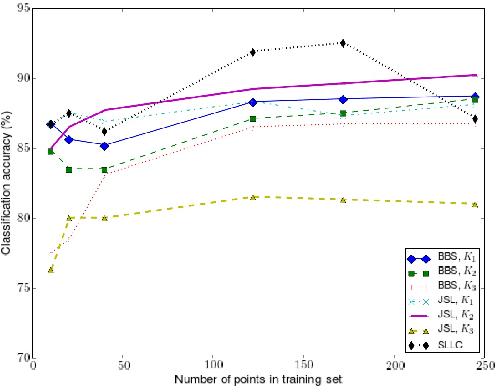
The notion of metric plays a key role in machine learning problems such as classification, clustering or ranking. However, it is worth noting that there is a severe lack of theoretical guarantees that can be expected on the generalization capacity of the classifier associated to a given metric. The theoretical framework of $(\epsilon, \gamma, \tau)$-good similarity functions (Balcan et al., 2008) has been one of the first attempts to draw a link between the properties of a similarity function and those of a linear classifier making use of it. In this paper, we extend and complete this theory by providing a new generalization bound for the associated classifier based on the algorithmic robustness framework.