Algorithmic Robustness for Learning via $(ε, γ, τ)$-Good Similarity Functions
Paper and Code
Mar 31, 2015
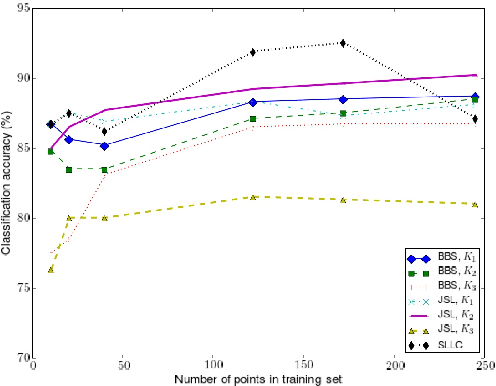

The notion of metric plays a key role in machine learning problems such as classification, clustering or ranking. However, it is worth noting that there is a severe lack of theoretical guarantees that can be expected on the generalization capacity of the classifier associated to a given metric. The theoretical framework of $(\epsilon, \gamma, \tau)$-good similarity functions (Balcan et al., 2008) has been one of the first attempts to draw a link between the properties of a similarity function and those of a linear classifier making use of it. In this paper, we extend and complete this theory by providing a new generalization bound for the associated classifier based on the algorithmic robustness framework.
* ICLR 2015 Workshop - accepted
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge