Class-Balance Bias in Regularized Regression

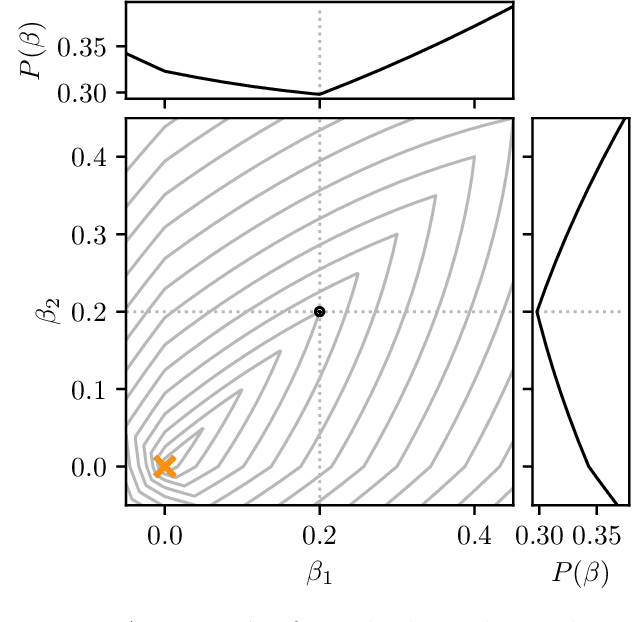
Regularized models are often sensitive to the scales of the features in the data and it has therefore become standard practice to normalize (center and scale) the features before fitting the model. But there are many different ways to normalize the features and the choice may have dramatic effects on the resulting model. In spite of this, there has so far been no research on this topic. In this paper, we begin to bridge this knowledge gap by studying normalization in the context of lasso, ridge, and elastic net regression. We focus on normal and binary features and show that the class balances of binary features directly influences the regression coefficients and that this effect depends on the combination of normalization and regularization methods used. We demonstrate that this effect can be mitigated by scaling binary features with their variance in the case of the lasso and standard deviation in the case of ridge regression, but that this comes at the cost of increased variance. For the elastic net, we show that scaling the penalty weights, rather than the features, can achieve the same effect. Finally, we also tackle mixes of binary and normal features as well as interactions and provide some initial results on how to normalize features in these cases.

Coordinate Descent for SLOPE

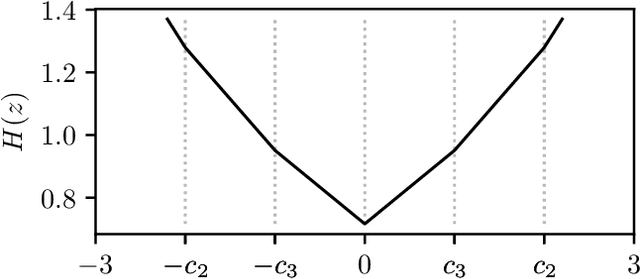
The lasso is the most famous sparse regression and feature selection method. One reason for its popularity is the speed at which the underlying optimization problem can be solved. Sorted L-One Penalized Estimation (SLOPE) is a generalization of the lasso with appealing statistical properties. In spite of this, the method has not yet reached widespread interest. A major reason for this is that current software packages that fit SLOPE rely on algorithms that perform poorly in high dimensions. To tackle this issue, we propose a new fast algorithm to solve the SLOPE optimization problem, which combines proximal gradient descent and proximal coordinate descent steps. We provide new results on the directional derivative of the SLOPE penalty and its related SLOPE thresholding operator, as well as provide convergence guarantees for our proposed solver. In extensive benchmarks on simulated and real data, we show that our method outperforms a long list of competing algorithms.

Efficient methods for Gaussian Markov random fields under sparse linear constraints

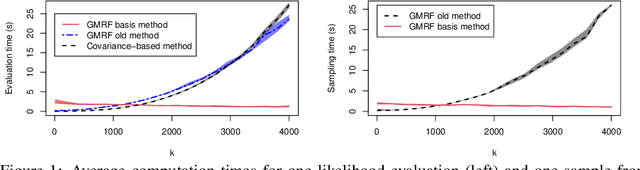
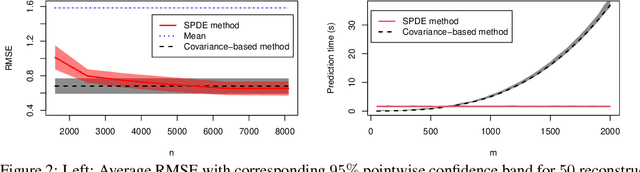
Methods for inference and simulation of linearly constrained Gaussian Markov Random Fields (GMRF) are computationally prohibitive when the number of constraints is large. In some cases, such as for intrinsic GMRFs, they may even be unfeasible. We propose a new class of methods to overcome these challenges in the common case of sparse constraints, where one has a large number of constraints and each only involves a few elements. Our methods rely on a basis transformation into blocks of constrained versus non-constrained subspaces, and we show that the methods greatly outperform existing alternatives in terms of computational cost. By combining the proposed methods with the stochastic partial differential equation approach for Gaussian random fields, we also show how to formulate Gaussian process regression with linear constraints in a GMRF setting to reduce computational cost. This is illustrated in two applications with simulated data.

The Hessian Screening Rule

Predictor screening rules, which discard predictors from the design matrix before fitting a model, have had sizable impacts on the speed with which $\ell_1$-regularized regression problems, such as the lasso, can be solved. Current state-of-the-art screening rules, however, have difficulties in dealing with highly-correlated predictors, often becoming too conservative. In this paper, we present a new screening rule to deal with this issue: the Hessian Screening Rule. The rule uses second-order information from the model in order to provide more accurate screening as well as higher-quality warm starts. In our experiments on $\ell_1$-regularized least-squares (the lasso) and logistic regression, we show that the rule outperforms all other alternatives in simulated experiments with high correlation, as well as in the majority of real datasets that we study.

The Strong Screening Rule for SLOPE

Extracting relevant features from data sets where the number of observations ($n$) is much smaller then the number of predictors ($p$) is a major challenge in modern statistics. Sorted L-One Penalized Estimation (SLOPE), a generalization of the lasso, is a promising method within this setting. Current numerical procedures for SLOPE, however, lack the efficiency that respective tools for the lasso enjoy, particularly in the context of estimating a complete regularization path. A key component in the efficiency of the lasso is predictor screening rules: rules that allow predictors to be discarded before estimating the model. This is the first paper to establish such a rule for SLOPE. We develop a screening rule for SLOPE by examining its subdifferential and show that this rule is a generalization of the strong rule for the lasso. Our rule is heuristic, which means that it may discard predictors erroneously. We present conditions under which this may happen and show that such situations are rare and easily safeguarded against by a simple check of the optimality conditions. Our numerical experiments show that the rule performs well in practice, leading to improvements by orders of magnitude for data in the $p \gg n$ domain, as well as incurring no additional computational overhead when $n \gg p$. We also examine the effect of correlation structures in the design matrix on the rule and discuss algorithmic strategies for employing the rule. Finally, we provide an efficient implementation of the rule in our R package SLOPE.

Whole-brain substitute CT generation using Markov random field mixture models

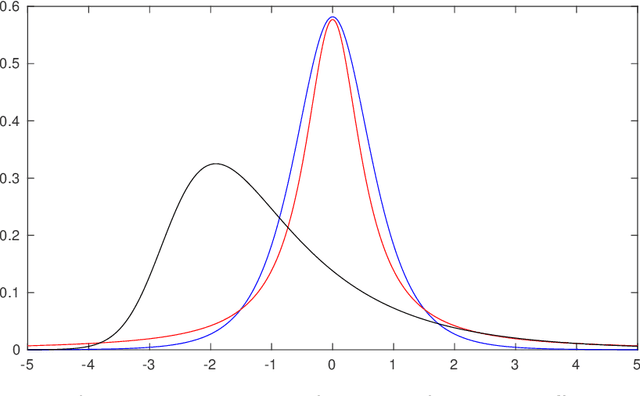
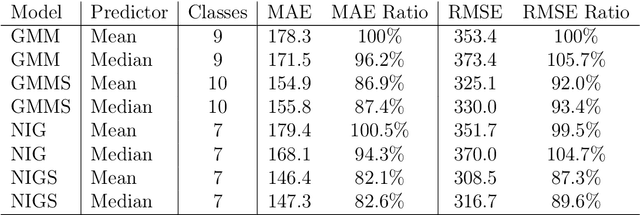
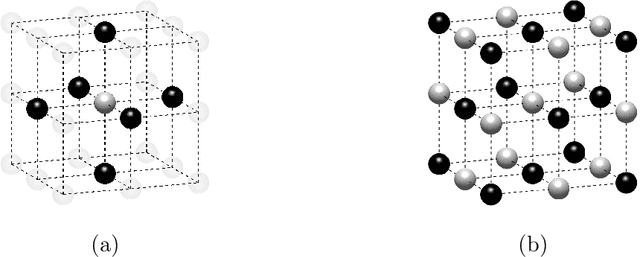
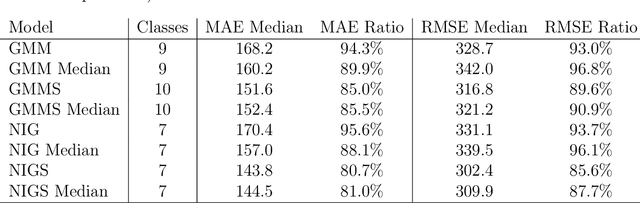
Computed tomography (CT) equivalent information is needed for attenuation correction in PET imaging and for dose planning in radiotherapy. Prior work has shown that Gaussian mixture models can be used to generate a substitute CT (s-CT) image from a specific set of MRI modalities. This work introduces a more flexible class of mixture models for s-CT generation, that incorporates spatial dependency in the data through a Markov random field prior on the latent field of class memberships associated with a mixture model. Furthermore, the mixture distributions are extended from Gaussian to normal inverse Gaussian (NIG), allowing heavier tails and skewness. The amount of data needed to train a model for s-CT generation is of the order of 100 million voxels. The computational efficiency of the parameter estimation and prediction methods are hence paramount, especially when spatial dependency is included in the models. A stochastic Expectation Maximization (EM) gradient algorithm is proposed in order to tackle this challenge. The advantages of the spatial model and NIG distributions are evaluated with a cross-validation study based on data from 14 patients. The study show that the proposed model enhances the predictive quality of the s-CT images by reducing the mean absolute error with 17.9%. Also, the distribution of CT values conditioned on the MR images are better explained by the proposed model as evaluated using continuous ranked probability scores.