Linear cost and exponentially convergent approximation of Gaussian Matérn processes

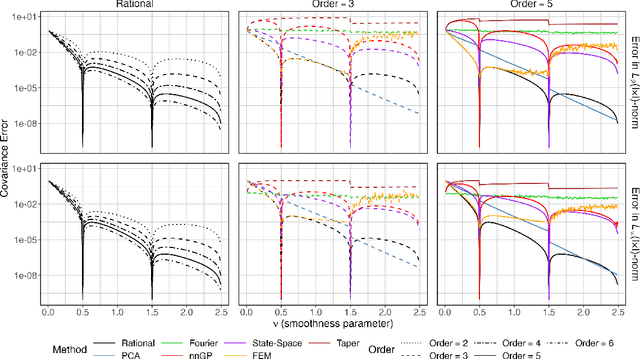
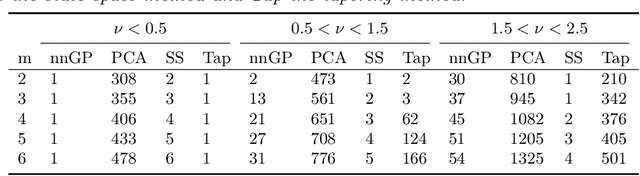
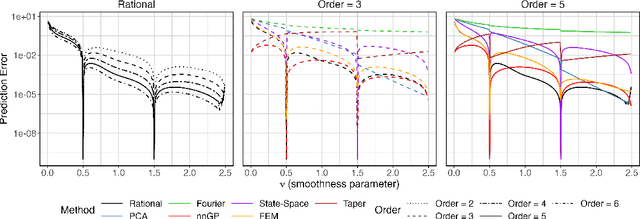
The computational cost for inference and prediction of statistical models based on Gaussian processes with Mat\'ern covariance functions scales cubicly with the number of observations, limiting their applicability to large data sets. The cost can be reduced in certain special cases, but there are currently no generally applicable exact methods with linear cost. Several approximate methods have been introduced to reduce the cost, but most of these lack theoretical guarantees for the accuracy. We consider Gaussian processes on bounded intervals with Mat\'ern covariance functions and for the first time develop a generally applicable method with linear cost and with a covariance error that decreases exponentially fast in the order $m$ of the proposed approximation. The method is based on an optimal rational approximation of the spectral density and results in an approximation that can be represented as a sum of $m$ independent Gaussian Markov processes, which facilitates easy usage in general software for statistical inference, enabling its efficient implementation in general statistical inference software packages. Besides the theoretical justifications, we demonstrate the accuracy empirically through carefully designed simulation studies which show that the method outperforms all state-of-the-art alternatives in terms of accuracy for a fixed computational cost in statistical tasks such as Gaussian process regression.

Efficient methods for Gaussian Markov random fields under sparse linear constraints

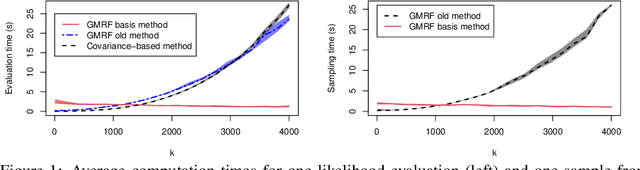
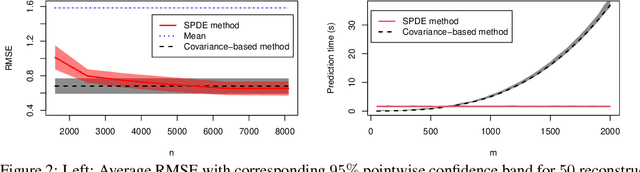
Methods for inference and simulation of linearly constrained Gaussian Markov Random Fields (GMRF) are computationally prohibitive when the number of constraints is large. In some cases, such as for intrinsic GMRFs, they may even be unfeasible. We propose a new class of methods to overcome these challenges in the common case of sparse constraints, where one has a large number of constraints and each only involves a few elements. Our methods rely on a basis transformation into blocks of constrained versus non-constrained subspaces, and we show that the methods greatly outperform existing alternatives in terms of computational cost. By combining the proposed methods with the stochastic partial differential equation approach for Gaussian random fields, we also show how to formulate Gaussian process regression with linear constraints in a GMRF setting to reduce computational cost. This is illustrated in two applications with simulated data.

Whole-brain substitute CT generation using Markov random field mixture models

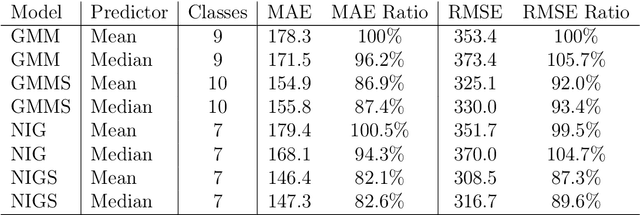
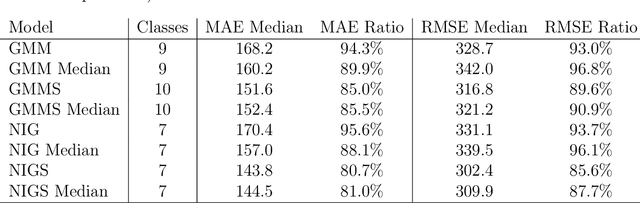
Computed tomography (CT) equivalent information is needed for attenuation correction in PET imaging and for dose planning in radiotherapy. Prior work has shown that Gaussian mixture models can be used to generate a substitute CT (s-CT) image from a specific set of MRI modalities. This work introduces a more flexible class of mixture models for s-CT generation, that incorporates spatial dependency in the data through a Markov random field prior on the latent field of class memberships associated with a mixture model. Furthermore, the mixture distributions are extended from Gaussian to normal inverse Gaussian (NIG), allowing heavier tails and skewness. The amount of data needed to train a model for s-CT generation is of the order of 100 million voxels. The computational efficiency of the parameter estimation and prediction methods are hence paramount, especially when spatial dependency is included in the models. A stochastic Expectation Maximization (EM) gradient algorithm is proposed in order to tackle this challenge. The advantages of the spatial model and NIG distributions are evaluated with a cross-validation study based on data from 14 patients. The study show that the proposed model enhances the predictive quality of the s-CT images by reducing the mean absolute error with 17.9%. Also, the distribution of CT values conditioned on the MR images are better explained by the proposed model as evaluated using continuous ranked probability scores.