Vaibhav Mehandiratta
Linear cost and exponentially convergent approximation of Gaussian Matérn processes
Oct 16, 2024
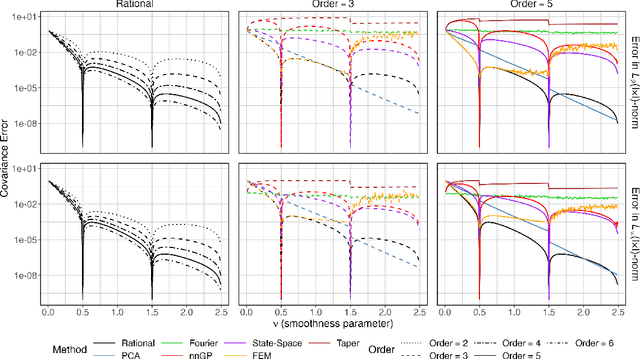
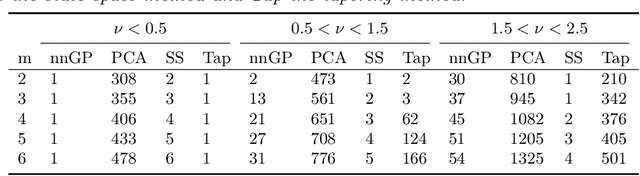
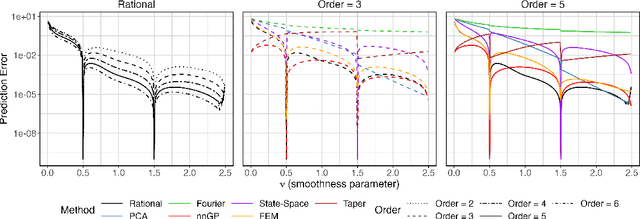
Abstract:The computational cost for inference and prediction of statistical models based on Gaussian processes with Mat\'ern covariance functions scales cubicly with the number of observations, limiting their applicability to large data sets. The cost can be reduced in certain special cases, but there are currently no generally applicable exact methods with linear cost. Several approximate methods have been introduced to reduce the cost, but most of these lack theoretical guarantees for the accuracy. We consider Gaussian processes on bounded intervals with Mat\'ern covariance functions and for the first time develop a generally applicable method with linear cost and with a covariance error that decreases exponentially fast in the order $m$ of the proposed approximation. The method is based on an optimal rational approximation of the spectral density and results in an approximation that can be represented as a sum of $m$ independent Gaussian Markov processes, which facilitates easy usage in general software for statistical inference, enabling its efficient implementation in general statistical inference software packages. Besides the theoretical justifications, we demonstrate the accuracy empirically through carefully designed simulation studies which show that the method outperforms all state-of-the-art alternatives in terms of accuracy for a fixed computational cost in statistical tasks such as Gaussian process regression.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge