Efficient methods for Gaussian Markov random fields under sparse linear constraints
Paper and Code
Jun 03, 2021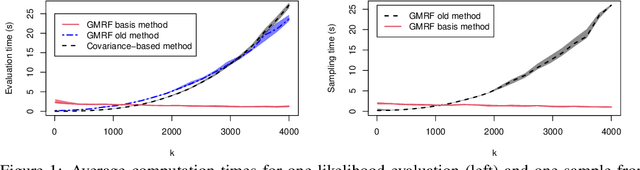
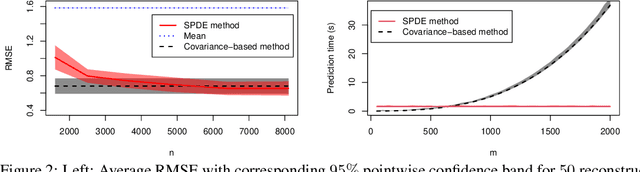
Methods for inference and simulation of linearly constrained Gaussian Markov Random Fields (GMRF) are computationally prohibitive when the number of constraints is large. In some cases, such as for intrinsic GMRFs, they may even be unfeasible. We propose a new class of methods to overcome these challenges in the common case of sparse constraints, where one has a large number of constraints and each only involves a few elements. Our methods rely on a basis transformation into blocks of constrained versus non-constrained subspaces, and we show that the methods greatly outperform existing alternatives in terms of computational cost. By combining the proposed methods with the stochastic partial differential equation approach for Gaussian random fields, we also show how to formulate Gaussian process regression with linear constraints in a GMRF setting to reduce computational cost. This is illustrated in two applications with simulated data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge