FedECA: A Federated External Control Arm Method for Causal Inference with Time-To-Event Data in Distributed Settings

External control arms (ECA) can inform the early clinical development of experimental drugs and provide efficacy evidence for regulatory approval in non-randomized settings. However, the main challenge of implementing ECA lies in accessing real-world data or historical clinical trials. Indeed, data sharing is often not feasible due to privacy considerations related to data leaving the original collection centers, along with pharmaceutical companies' competitive motives. In this paper, we leverage a privacy-enhancing technology called federated learning (FL) to remove some of the barriers to data sharing. We introduce a federated learning inverse probability of treatment weighted (IPTW) method for time-to-event outcomes called FedECA which eases the implementation of ECA by limiting patients' data exposure. We show with extensive experiments that FedECA outperforms its closest competitor, matching-adjusted indirect comparison (MAIC), in terms of statistical power and ability to balance the treatment and control groups. To encourage the use of such methods, we publicly release our code which relies on Substra, an open-source FL software with proven experience in privacy-sensitive contexts.

Coordinate Descent for SLOPE

The lasso is the most famous sparse regression and feature selection method. One reason for its popularity is the speed at which the underlying optimization problem can be solved. Sorted L-One Penalized Estimation (SLOPE) is a generalization of the lasso with appealing statistical properties. In spite of this, the method has not yet reached widespread interest. A major reason for this is that current software packages that fit SLOPE rely on algorithms that perform poorly in high dimensions. To tackle this issue, we propose a new fast algorithm to solve the SLOPE optimization problem, which combines proximal gradient descent and proximal coordinate descent steps. We provide new results on the directional derivative of the SLOPE penalty and its related SLOPE thresholding operator, as well as provide convergence guarantees for our proposed solver. In extensive benchmarks on simulated and real data, we show that our method outperforms a long list of competing algorithms.

Benchopt: Reproducible, efficient and collaborative optimization benchmarks

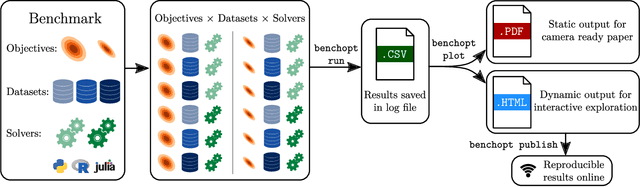
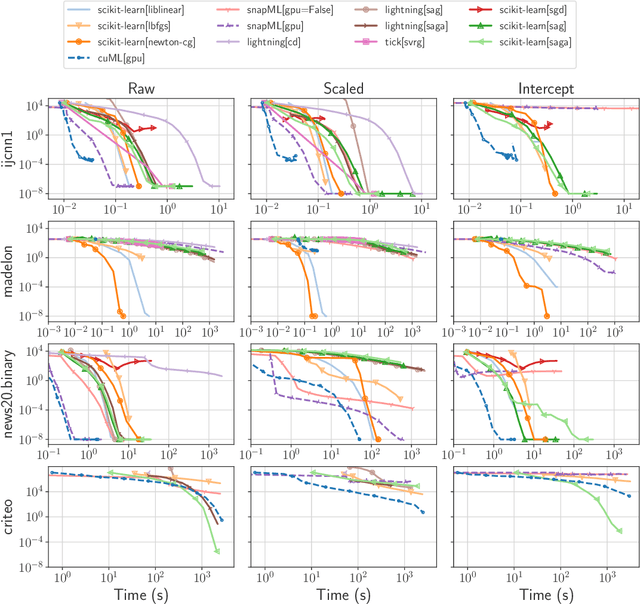
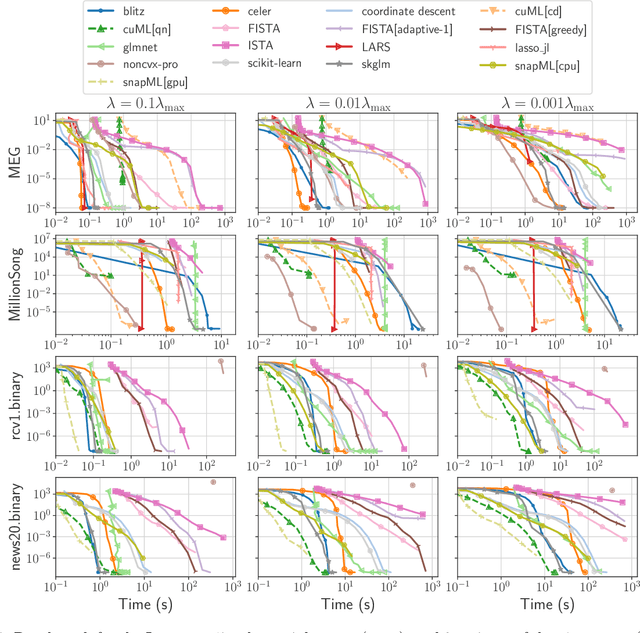
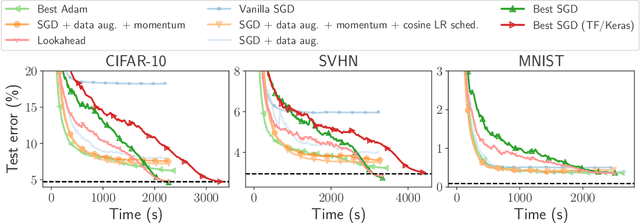
Numerical validation is at the core of machine learning research as it allows to assess the actual impact of new methods, and to confirm the agreement between theory and practice. Yet, the rapid development of the field poses several challenges: researchers are confronted with a profusion of methods to compare, limited transparency and consensus on best practices, as well as tedious re-implementation work. As a result, validation is often very partial, which can lead to wrong conclusions that slow down the progress of research. We propose Benchopt, a collaborative framework to automate, reproduce and publish optimization benchmarks in machine learning across programming languages and hardware architectures. Benchopt simplifies benchmarking for the community by providing an off-the-shelf tool for running, sharing and extending experiments. To demonstrate its broad usability, we showcase benchmarks on three standard learning tasks: $\ell_2$-regularized logistic regression, Lasso, and ResNet18 training for image classification. These benchmarks highlight key practical findings that give a more nuanced view of the state-of-the-art for these problems, showing that for practical evaluation, the devil is in the details. We hope that Benchopt will foster collaborative work in the community hence improving the reproducibility of research findings.

Beyond L1: Faster and Better Sparse Models with skglm

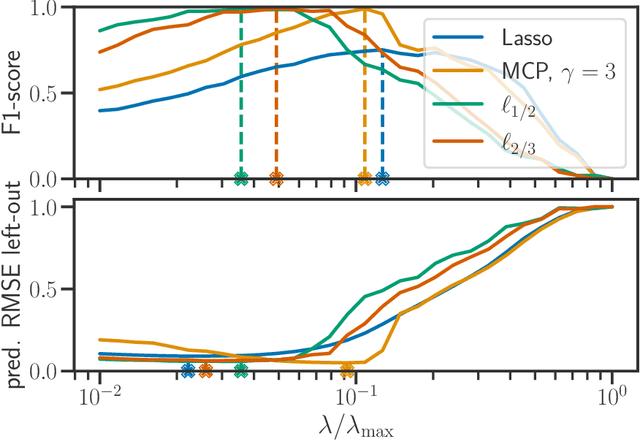
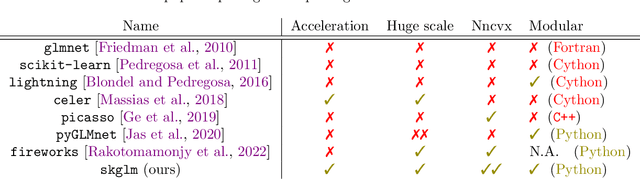
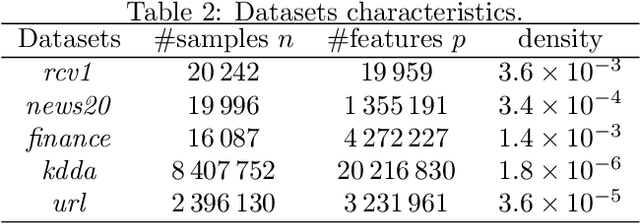
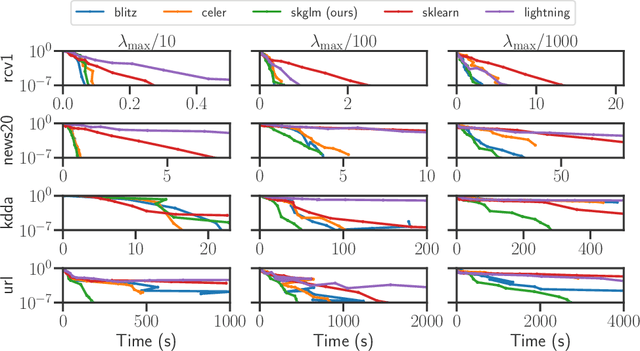
We propose a new fast algorithm to estimate any sparse generalized linear model with convex or non-convex separable penalties. Our algorithm is able to solve problems with millions of samples and features in seconds, by relying on coordinate descent, working sets and Anderson acceleration. It handles previously unaddressed models, and is extensively shown to improve state-of-art algorithms. We provide a flexible, scikit-learn compatible package, which easily handles customized datafits and penalties.

Implicit differentiation for fast hyperparameter selection in non-smooth convex learning

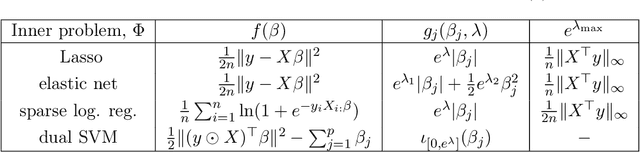
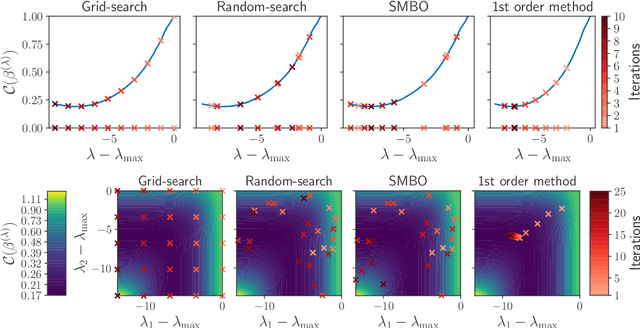
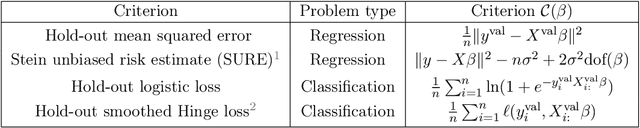
Finding the optimal hyperparameters of a model can be cast as a bilevel optimization problem, typically solved using zero-order techniques. In this work we study first-order methods when the inner optimization problem is convex but non-smooth. We show that the forward-mode differentiation of proximal gradient descent and proximal coordinate descent yield sequences of Jacobians converging toward the exact Jacobian. Using implicit differentiation, we show it is possible to leverage the non-smoothness of the inner problem to speed up the computation. Finally, we provide a bound on the error made on the hypergradient when the inner optimization problem is solved approximately. Results on regression and classification problems reveal computational benefits for hyperparameter optimization, especially when multiple hyperparameters are required.

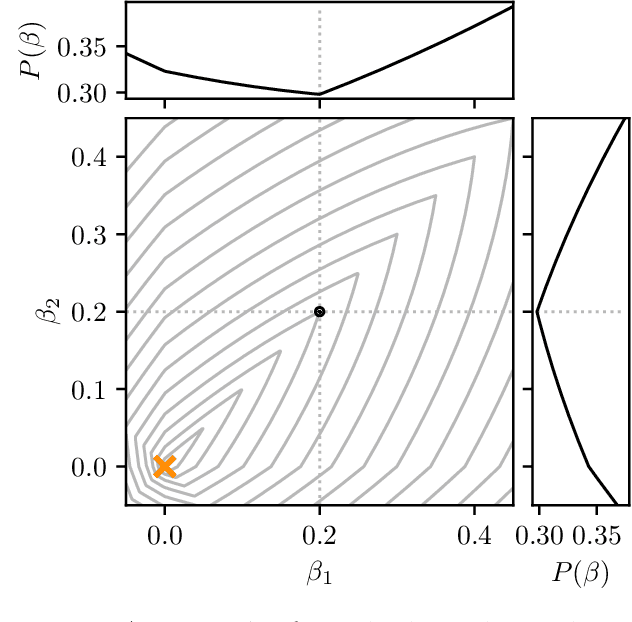
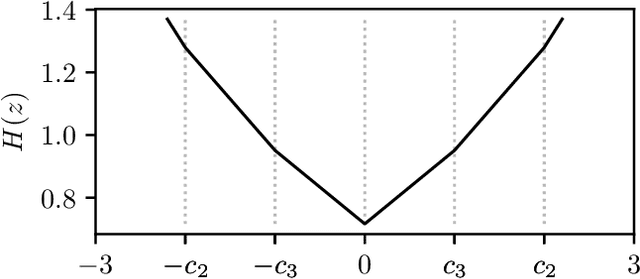
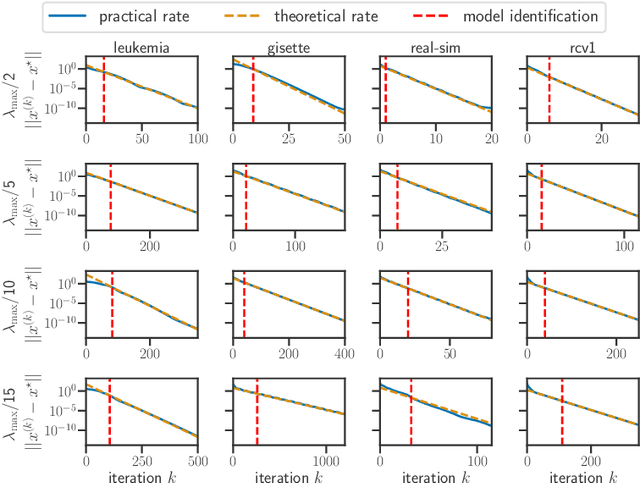
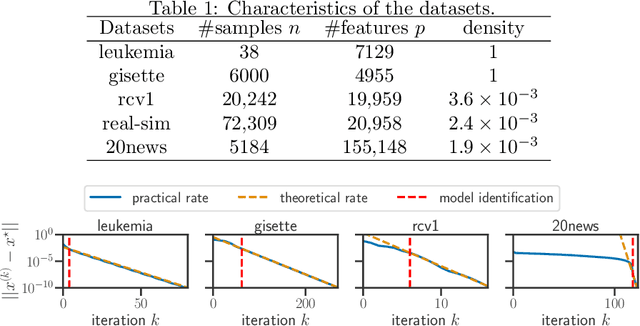
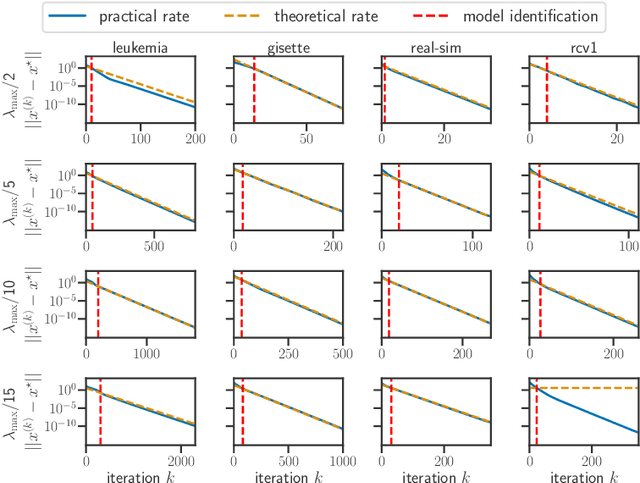
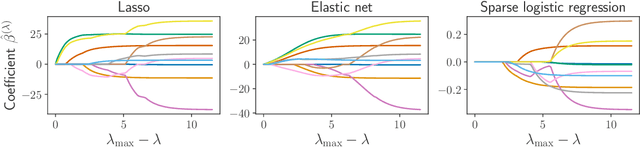
Model identification and local linear convergence of coordinate descent

For composite nonsmooth optimization problems, Forward-Backward algorithm achieves model identification (e.g. support identification for the Lasso) after a finite number of iterations, provided the objective function is regular enough. Results concerning coordinate descent are scarcer and model identification has only been shown for specific estimators, the support-vector machine for instance. In this work, we show that cyclic coordinate descent achieves model identification in finite time for a wide class of functions. In addition, we prove explicit local linear convergence rates for coordinate descent. Extensive experiments on various estimators and on real datasets demonstrate that these rates match well empirical results.

Implicit differentiation of Lasso-type models for hyperparameter optimization

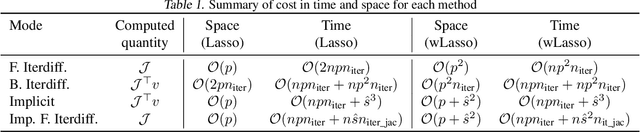
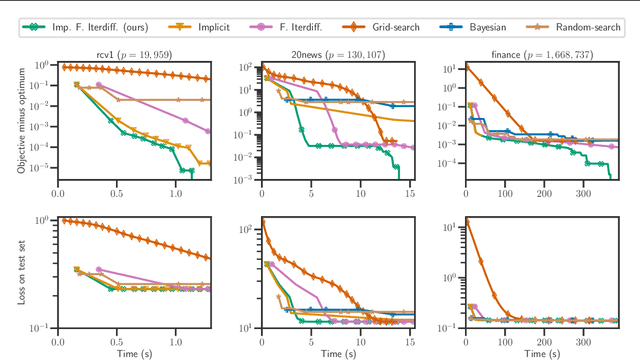
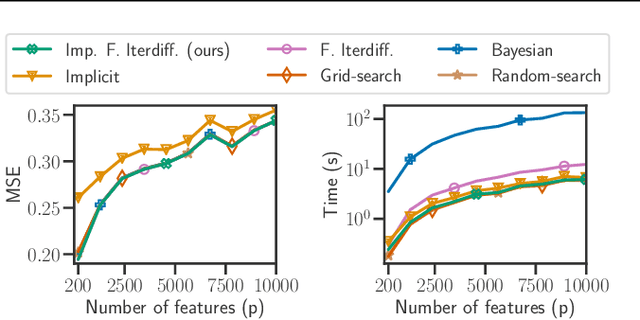
Setting regularization parameters for Lasso-type estimators is notoriously difficult, though crucial in practice. The most popular hyperparameter optimization approach is grid-search using held-out validation data. Grid-search however requires to choose a predefined grid for each parameter, which scales exponentially in the number of parameters. Another approach is to cast hyperparameter optimization as a bi-level optimization problem, one can solve by gradient descent. The key challenge for these methods is the estimation of the gradient with respect to the hyperparameters. Computing this gradient via forward or backward automatic differentiation is possible yet usually suffers from high memory consumption. Alternatively implicit differentiation typically involves solving a linear system which can be prohibitive and numerically unstable in high dimension. In addition, implicit differentiation usually assumes smooth loss functions, which is not the case for Lasso-type problems. This work introduces an efficient implicit differentiation algorithm, without matrix inversion, tailored for Lasso-type problems. Our approach scales to high-dimensional data by leveraging the sparsity of the solutions. Experiments demonstrate that the proposed method outperforms a large number of standard methods to optimize the error on held-out data, or the Stein Unbiased Risk Estimator (SURE).

Linear Support Vector Regression with Linear Constraints

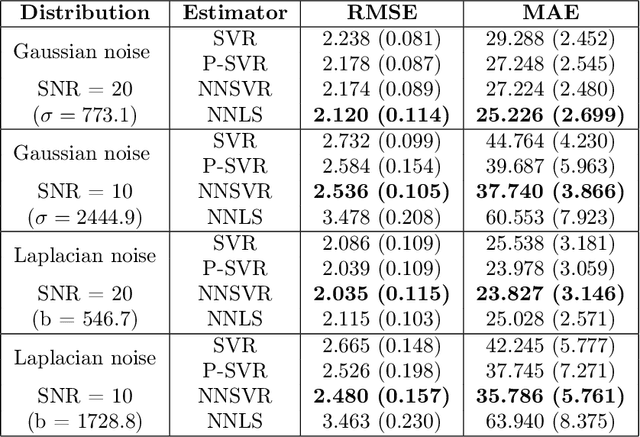
This paper studies the addition of linear constraints to the Support Vector Regression (SVR) when the kernel is linear. Adding those constraints into the problem allows to add prior knowledge on the estimator obtained, such as finding probability vector or monotone data. We propose a generalization of the Sequential Minimal Optimization (SMO) algorithm for solving the optimization problem with linear constraints and prove its convergence. Then, practical performances of this estimator are shown on simulated and real datasets with different settings: non negative regression, regression onto the simplex for biomedical data and isotonic regression for weather forecast.