Linear Support Vector Regression with Linear Constraints
Paper and Code
Nov 06, 2019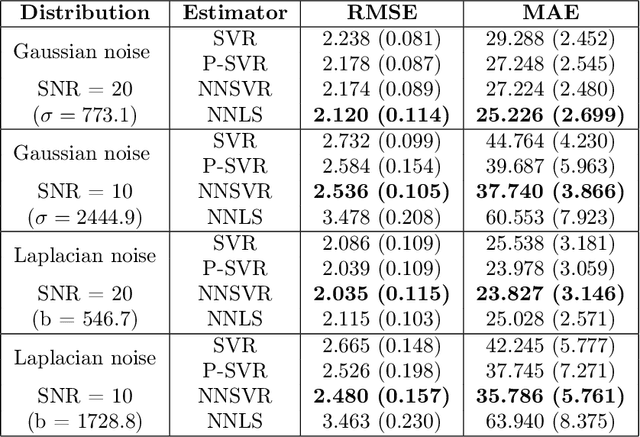



This paper studies the addition of linear constraints to the Support Vector Regression (SVR) when the kernel is linear. Adding those constraints into the problem allows to add prior knowledge on the estimator obtained, such as finding probability vector or monotone data. We propose a generalization of the Sequential Minimal Optimization (SMO) algorithm for solving the optimization problem with linear constraints and prove its convergence. Then, practical performances of this estimator are shown on simulated and real datasets with different settings: non negative regression, regression onto the simplex for biomedical data and isotonic regression for weather forecast.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge