A Near-Optimal Algorithm for Bilevel Empirical Risk Minimization

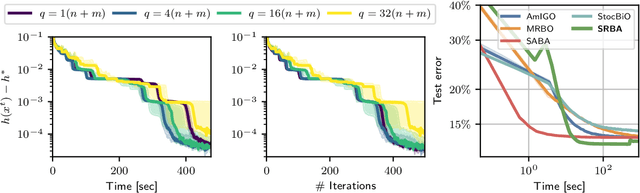
Bilevel optimization problems, which are problems where two optimization problems are nested, have more and more applications in machine learning. In many practical cases, the upper and the lower objectives correspond to empirical risk minimization problems and therefore have a sum structure. In this context, we propose a bilevel extension of the celebrated SARAH algorithm. We demonstrate that the algorithm requires $\mathcal{O}((n+m)^{\frac12}\varepsilon^{-1})$ gradient computations to achieve $\varepsilon$-stationarity with $n+m$ the total number of samples, which improves over all previous bilevel algorithms. Moreover, we provide a lower bound on the number of oracle calls required to get an approximate stationary point of the objective function of the bilevel problem. This lower bound is attained by our algorithm, which is therefore optimal in terms of sample complexity.

Benchopt: Reproducible, efficient and collaborative optimization benchmarks

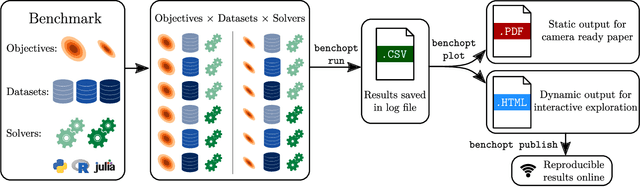
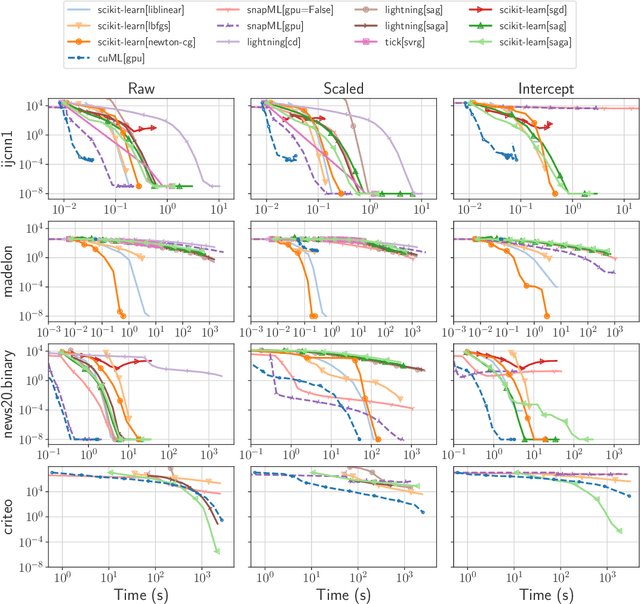
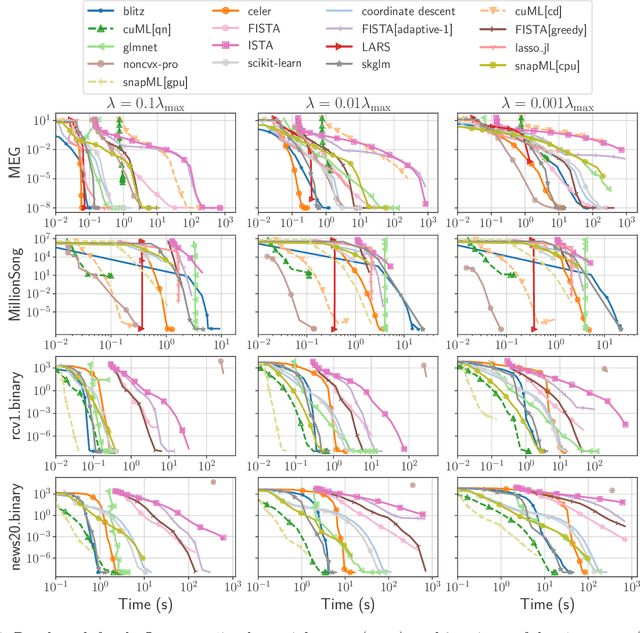
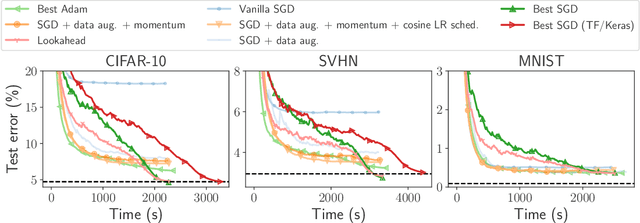
Numerical validation is at the core of machine learning research as it allows to assess the actual impact of new methods, and to confirm the agreement between theory and practice. Yet, the rapid development of the field poses several challenges: researchers are confronted with a profusion of methods to compare, limited transparency and consensus on best practices, as well as tedious re-implementation work. As a result, validation is often very partial, which can lead to wrong conclusions that slow down the progress of research. We propose Benchopt, a collaborative framework to automate, reproduce and publish optimization benchmarks in machine learning across programming languages and hardware architectures. Benchopt simplifies benchmarking for the community by providing an off-the-shelf tool for running, sharing and extending experiments. To demonstrate its broad usability, we showcase benchmarks on three standard learning tasks: $\ell_2$-regularized logistic regression, Lasso, and ResNet18 training for image classification. These benchmarks highlight key practical findings that give a more nuanced view of the state-of-the-art for these problems, showing that for practical evaluation, the devil is in the details. We hope that Benchopt will foster collaborative work in the community hence improving the reproducibility of research findings.

A framework for bilevel optimization that enables stochastic and global variance reduction algorithms

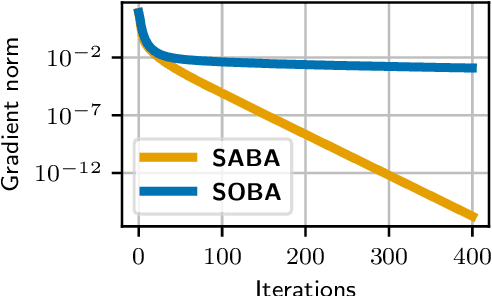
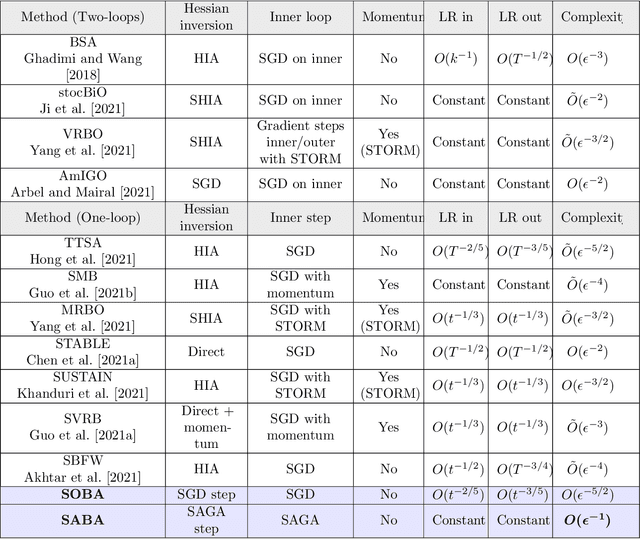
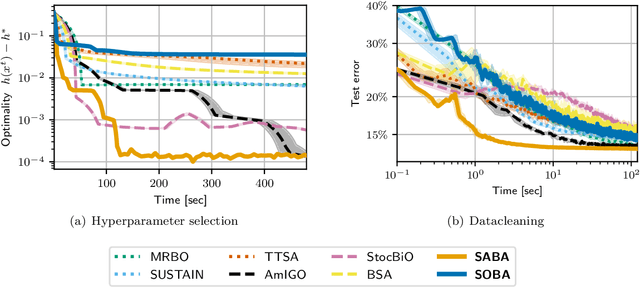
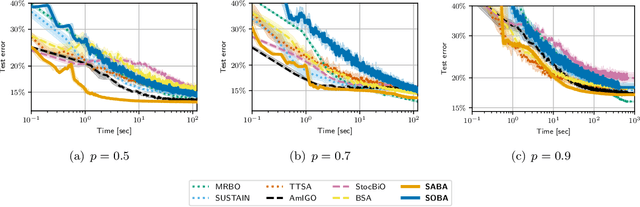
Bilevel optimization, the problem of minimizing a value function which involves the arg-minimum of another function, appears in many areas of machine learning. In a large scale setting where the number of samples is huge, it is crucial to develop stochastic methods, which only use a few samples at a time to progress. However, computing the gradient of the value function involves solving a linear system, which makes it difficult to derive unbiased stochastic estimates. To overcome this problem we introduce a novel framework, in which the solution of the inner problem, the solution of the linear system, and the main variable evolve at the same time. These directions are written as a sum, making it straightforward to derive unbiased estimates. The simplicity of our approach allows us to develop global variance reduction algorithms, where the dynamics of all variables is subject to variance reduction. We demonstrate that SABA, an adaptation of the celebrated SAGA algorithm in our framework, has $O(\frac1T)$ convergence rate, and that it achieves linear convergence under Polyak-Lojasciewicz assumption. This is the first stochastic algorithm for bilevel optimization that verifies either of these properties. Numerical experiments validate the usefulness of our method.