Model identification and local linear convergence of coordinate descent
Paper and Code
Oct 22, 2020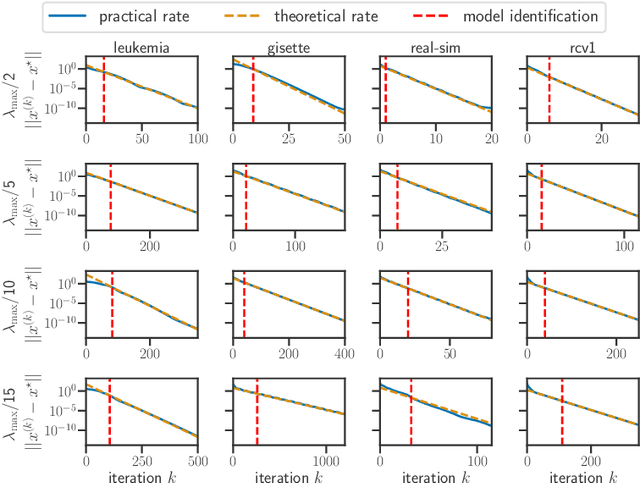
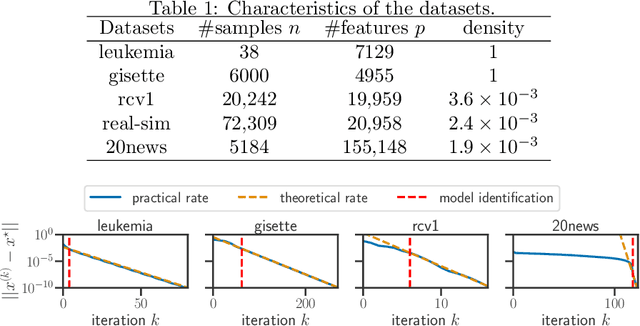
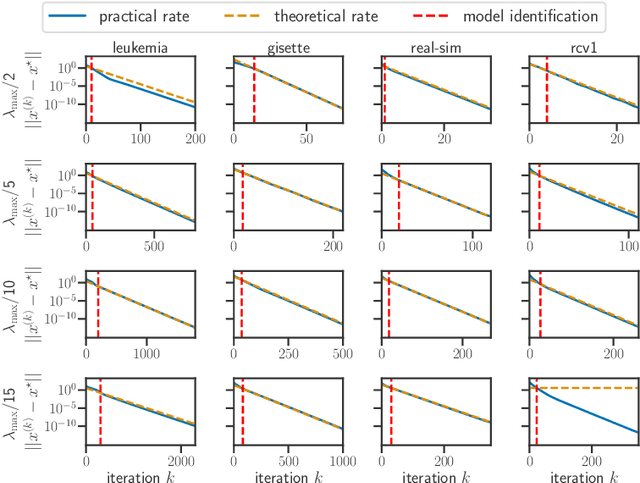
For composite nonsmooth optimization problems, Forward-Backward algorithm achieves model identification (e.g. support identification for the Lasso) after a finite number of iterations, provided the objective function is regular enough. Results concerning coordinate descent are scarcer and model identification has only been shown for specific estimators, the support-vector machine for instance. In this work, we show that cyclic coordinate descent achieves model identification in finite time for a wide class of functions. In addition, we prove explicit local linear convergence rates for coordinate descent. Extensive experiments on various estimators and on real datasets demonstrate that these rates match well empirical results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge