Non-Redundant Combination of Hand-Crafted and Deep Learning Radiomics: Application to the Early Detection of Pancreatic Cancer

We address the problem of learning Deep Learning Radiomics (DLR) that are not redundant with Hand-Crafted Radiomics (HCR). To do so, we extract DLR features using a VAE while enforcing their independence with HCR features by minimizing their mutual information. The resulting DLR features can be combined with hand-crafted ones and leveraged by a classifier to predict early markers of cancer. We illustrate our method on four early markers of pancreatic cancer and validate it on a large independent test set. Our results highlight the value of combining non-redundant DLR and HCR features, as evidenced by an improvement in the Area Under the Curve compared to baseline methods that do not address redundancy or solely rely on HCR features.

Weakly-supervised positional contrastive learning: application to cirrhosis classification

Large medical imaging datasets can be cheaply and quickly annotated with low-confidence, weak labels (e.g., radiological scores). Access to high-confidence labels, such as histology-based diagnoses, is rare and costly. Pretraining strategies, like contrastive learning (CL) methods, can leverage unlabeled or weakly-annotated datasets. These methods typically require large batch sizes, which poses a difficulty in the case of large 3D images at full resolution, due to limited GPU memory. Nevertheless, volumetric positional information about the spatial context of each 2D slice can be very important for some medical applications. In this work, we propose an efficient weakly-supervised positional (WSP) contrastive learning strategy where we integrate both the spatial context of each 2D slice and a weak label via a generic kernel-based loss function. We illustrate our method on cirrhosis prediction using a large volume of weakly-labeled images, namely radiological low-confidence annotations, and small strongly-labeled (i.e., high-confidence) datasets. The proposed model improves the classification AUC by 5% with respect to a baseline model on our internal dataset, and by 26% on the public LIHC dataset from the Cancer Genome Atlas. The code is available at: https://github.com/Guerbet-AI/wsp-contrastive.

Learning distributions of shape trajectories from longitudinal datasets: a hierarchical model on a manifold of diffeomorphisms

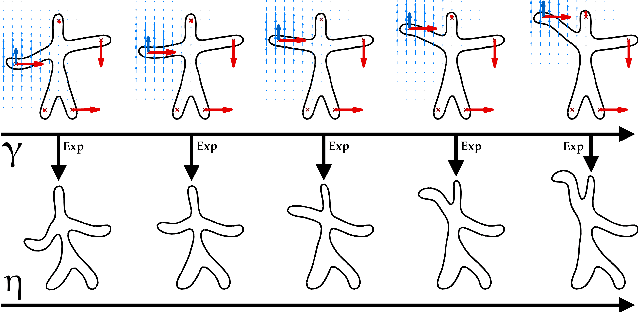
We propose a method to learn a distribution of shape trajectories from longitudinal data, i.e. the collection of individual objects repeatedly observed at multiple time-points. The method allows to compute an average spatiotemporal trajectory of shape changes at the group level, and the individual variations of this trajectory both in terms of geometry and time dynamics. First, we formulate a non-linear mixed-effects statistical model as the combination of a generic statistical model for manifold-valued longitudinal data, a deformation model defining shape trajectories via the action of a finite-dimensional set of diffeomorphisms with a manifold structure, and an efficient numerical scheme to compute parallel transport on this manifold. Second, we introduce a MCMC-SAEM algorithm with a specific approach to shape sampling, an adaptive scheme for proposal variances, and a log-likelihood tempering strategy to estimate our model. Third, we validate our algorithm on 2D simulated data, and then estimate a scenario of alteration of the shape of the hippocampus 3D brain structure during the course of Alzheimer's disease. The method shows for instance that hippocampal atrophy progresses more quickly in female subjects, and occurs earlier in APOE4 mutation carriers. We finally illustrate the potential of our method for classifying pathological trajectories versus normal ageing.

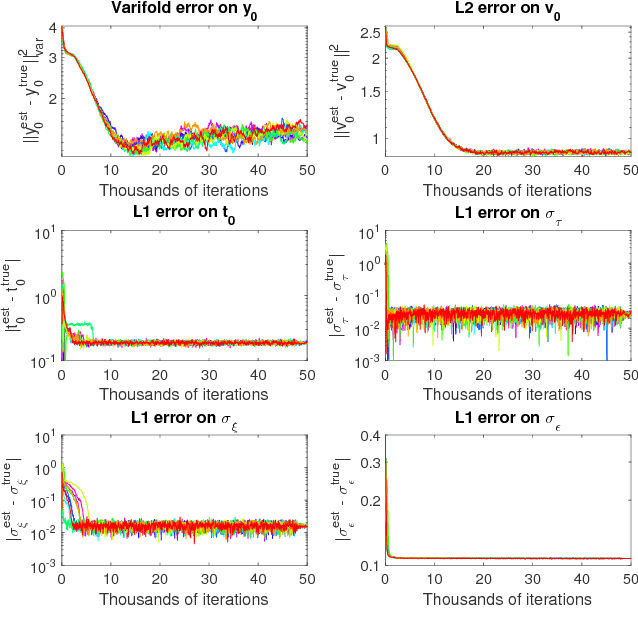
Parallel transport in shape analysis: a scalable numerical scheme

The analysis of manifold-valued data requires efficient tools from Riemannian geometry to cope with the computational complexity at stake. This complexity arises from the always-increasing dimension of the data, and the absence of closed-form expressions to basic operations such as the Riemannian logarithm. In this paper, we adapt a generic numerical scheme recently introduced for computing parallel transport along geodesics in a Riemannian manifold to finite-dimensional manifolds of diffeomorphisms. We provide a qualitative and quantitative analysis of its behavior on high-dimensional manifolds, and investigate an application with the prediction of brain structures progression.

Prediction of the progression of subcortical brain structures in Alzheimer's disease from baseline

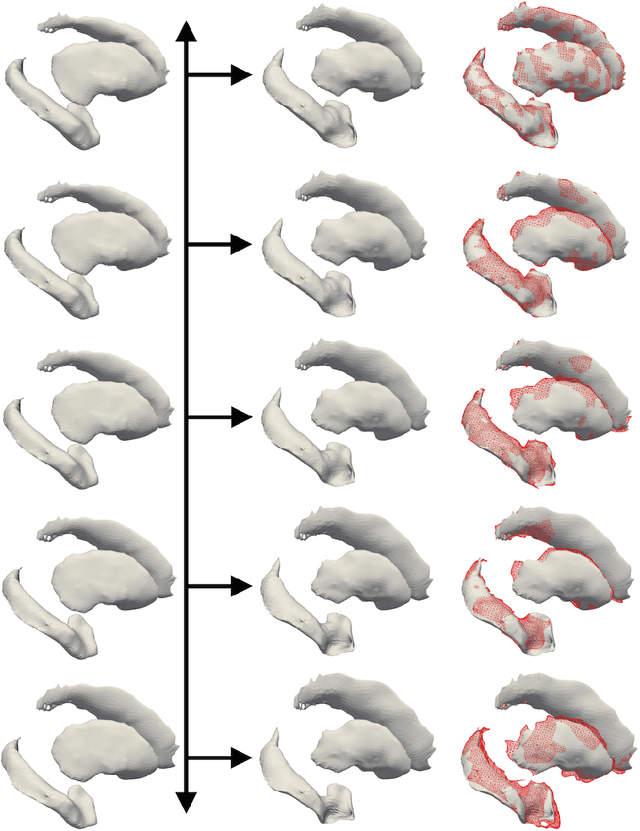
We propose a method to predict the subject-specific longitudinal progression of brain structures extracted from baseline MRI, and evaluate its performance on Alzheimer's disease data. The disease progression is modeled as a trajectory on a group of diffeomorphisms in the context of large deformation diffeomorphic metric mapping (LDDMM). We first exhibit the limited predictive abilities of geodesic regression extrapolation on this group. Building on the recent concept of parallel curves in shape manifolds, we then introduce a second predictive protocol which personalizes previously learned trajectories to new subjects, and investigate the relative performances of two parallel shifting paradigms. This design only requires the baseline imaging data. Finally, coefficients encoding the disease dynamics are obtained from longitudinal cognitive measurements for each subject, and exploited to refine our methodology which is demonstrated to successfully predict the follow-up visits.