Robostral Navigate

Deploying navigation systems at scale requires a recipe that minimizes sensor assumptions, generalizes across robot embodiments, and trains efficiently. Yet, today's best systems depend on depth sensors, multi-camera rigs, or pre-built maps, limiting the hardware they support and increasing deployment cost. We introduce Robostral Navigate, an 8B vision-language model built around this scalability objective. The model consumes only a stream of monocular RGB images - the most ubiquitous sensor across robotic platforms and predicts waypoints by pointing to the next target location in the current camera view. Operating purely in image space, rather than robot-specific coordinates, makes the policy naturally robust to changes in camera intrinsics and scene scale, enabling deployment across wheeled, legged, and aerial robots without recalibration. We generate 2.4 million trajectories across 350k simulated scenes to reduce the reliance on real-world data collection and scale easily. We further introduce a prefix-caching training recipe that packs entire episodes into single training sequences, reducing training tokens by 22x and cutting training time from months to days. A tree-based attention mask prevents conditioning on previous ground-truth actions, encouraging visually grounded action prediction, and reinforcement learning is used to further improve exploration and recovery capabilities. On the Room-to-Room and Room-Across-Room in Continuous Environments (R2R-CE and RxR-CE) benchmarks, Robostral Navigate sets a new state of the art. On R2R-CE, it achieves a 77.4% success rate, surpassing the best monocular method by 10.5 points and the strongest depth- or multi-camera system by 5.3 points despite using only a single RGB camera. On RxR-CE, it reaches 75.1% success rate, outperforming all monocular baselines.

On the Challenges and Opportunities of Learned Sparse Retrieval for Code

Retrieval over large codebases is a key component of modern LLM-based software engineering systems. Existing approaches predominantly rely on dense embedding models, while learned sparse retrieval (LSR) remains largely unexplored for code. However, applying sparse retrieval to code is challenging due to subword fragmentation, semantic gaps between natural-language queries and code, diversity of programming languages and sub-tasks, and the length of code documents, which can harm sparsity and latency. We introduce SPLADE-Code, the first large-scale family of learned sparse retrieval models specialized for code retrieval (600M-8B parameters). Despite a lightweight one-stage training pipeline, SPLADE-Code achieves state-of-the-art performance among retrievers under 1B parameters (75.4 on MTEB Code) and competitive results at larger scales (79.0 with 8B). We show that learned expansion tokens are critical to bridge lexical and semantic matching, and provide a latency analysis showing that LSR enables sub-millisecond retrieval on a 1M-passage collection with little effectiveness loss.

Naver Labs Europe @ WSDM CUP | Multilingual Retrieval

This report presents our participation to the WSDM Cup 2026 shared task on multilingual document retrieval from English queries. The task provides a challenging benchmark for cross-lingual generalization. It also provides a natural testbed for evaluating SPLARE, our recently proposed learned sparse retrieval model, which produces generalizable sparse latent representations and is particularly well suited to multilingual retrieval settings. We evaluate five progressively enhanced runs, starting from a SPLARE-7B model and incorporating lightweight improvements, including reranking with Qwen3-Reranker-4B and simple score fusion strategies. Our results demonstrate the strength of SPLARE compared to state-of-the-art dense baselines such as Qwen3-8B-Embed. More broadly, our submission highlights the continued relevance and competitiveness of learned sparse retrieval models beyond English-centric scenarios.

DiffLoRA: Differential Low-Rank Adapters for Large Language Models

Differential Transformer has recently been proposed to improve performance in Transformer models by canceling out noise through a denoiser attention mechanism. In this work, we introduce DiffLoRA, a parameter-efficient adaptation of the differential attention mechanism, with low-rank adapters on both positive and negative attention terms. This approach retains the efficiency of LoRA while aiming to benefit from the performance gains of differential attention. We evaluate DiffLoRA across a broad range of NLP tasks, including general benchmarks, many-shot in-context learning, RAG, and long-context tests. We observe that, although DiffLoRA falls short of other parameter-efficient fine-tuning methods in most evaluation tasks, it shows interesting results in certain domains (+11 pts on LoRA for HumanEval). We analyze the attention patterns post-finetuning to identify the reasons for this behavior.

Adapting Large Language Models for Multi-Domain Retrieval-Augmented-Generation

Retrieval-Augmented Generation (RAG) enhances LLM factuality, but multi-domain applications face challenges like lack of diverse benchmarks and poor out-of-domain generalization. The first contribution of this work is to introduce a diverse benchmark comprising a variety of question-answering tasks from 8 sources and covering 13 domains. Our second contribution consists in systematically testing out-of-domain generalization for typical RAG tuning strategies. While our findings reveal that standard fine-tuning fails to generalize effectively, we show that sequence-level distillation with teacher-generated labels improves out-of-domain performance by providing more coherent supervision. Our findings highlight key strategies for improving multi-domain RAG robustness.

PISCO: Pretty Simple Compression for Retrieval-Augmented Generation

Retrieval-Augmented Generation (RAG) pipelines enhance Large Language Models (LLMs) by retrieving relevant documents, but they face scalability issues due to high inference costs and limited context size. Document compression is a practical solution, but current soft compression methods suffer from accuracy losses and require extensive pretraining. In this paper, we introduce PISCO, a novel method that achieves a 16x compression rate with minimal accuracy loss (0-3%) across diverse RAG-based question-answering (QA) tasks. Unlike existing approaches, PISCO requires no pretraining or annotated data, relying solely on sequence-level knowledge distillation from document-based questions. With the ability to fine-tune a 7-10B LLM in 48 hours on a single A100 GPU, PISCO offers a highly efficient and scalable solution. We present comprehensive experiments showing that PISCO outperforms existing compression models by 8% in accuracy.

End-to-end Offline Reinforcement Learning for Glycemia Control

The development of closed-loop systems for glycemia control in type I diabetes relies heavily on simulated patients. Improving the performances and adaptability of these close-loops raises the risk of over-fitting the simulator. This may have dire consequences, especially in unusual cases which were not faithfully-if at all-captured by the simulator. To address this, we propose to use offline RL agents, trained on real patient data, to perform the glycemia control. To further improve the performances, we propose an end-to-end personalization pipeline, which leverages offline-policy evaluation methods to remove altogether the need of a simulator, while still enabling an estimation of clinically relevant metrics for diabetes.

Leveraging 3D Information in Unsupervised Brain MRI Segmentation

Automatic segmentation of brain abnormalities is challenging, as they vary considerably from one pathology to another. Current methods are supervised and require numerous annotated images for each pathology, a strenuous task. To tackle anatomical variability, Unsupervised Anomaly Detection (UAD) methods are proposed, detecting anomalies as outliers of a healthy model learned using a Variational Autoencoder (VAE). Previous work on UAD adopted a 2D approach, meaning that MRIs are processed as a collection of independent slices. Yet, it does not fully exploit the spatial information contained in MRI. Here, we propose to perform UAD in a 3D fashion and compare 2D and 3D VAEs. As a side contribution, we present a new loss function guarantying a robust training. Learning is performed using a multicentric dataset of healthy brain MRIs, and segmentation performances are estimated on White-Matter Hyperintensities and tumors lesions. Experiments demonstrate the interest of 3D methods which outperform their 2D counterparts.

Parallel transport in shape analysis: a scalable numerical scheme

The analysis of manifold-valued data requires efficient tools from Riemannian geometry to cope with the computational complexity at stake. This complexity arises from the always-increasing dimension of the data, and the absence of closed-form expressions to basic operations such as the Riemannian logarithm. In this paper, we adapt a generic numerical scheme recently introduced for computing parallel transport along geodesics in a Riemannian manifold to finite-dimensional manifolds of diffeomorphisms. We provide a qualitative and quantitative analysis of its behavior on high-dimensional manifolds, and investigate an application with the prediction of brain structures progression.

Prediction of the progression of subcortical brain structures in Alzheimer's disease from baseline

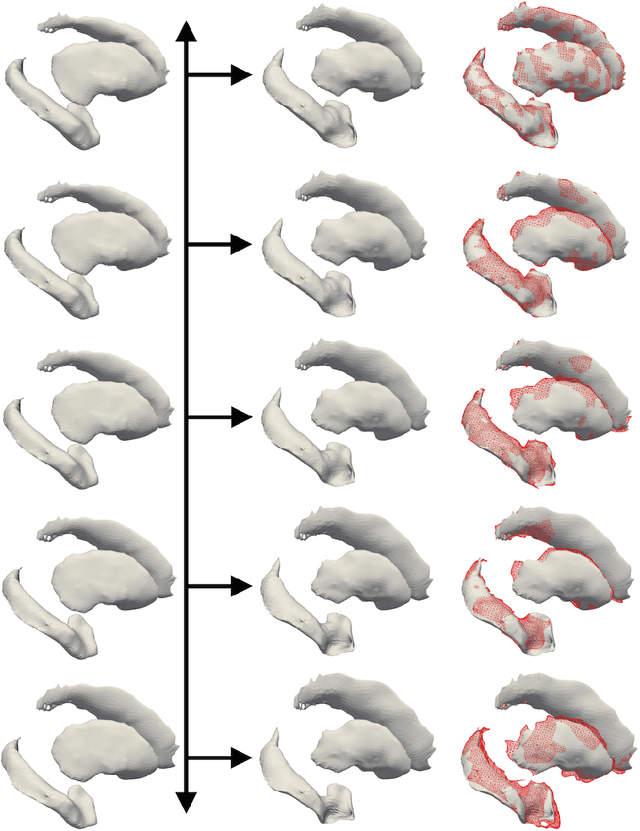
We propose a method to predict the subject-specific longitudinal progression of brain structures extracted from baseline MRI, and evaluate its performance on Alzheimer's disease data. The disease progression is modeled as a trajectory on a group of diffeomorphisms in the context of large deformation diffeomorphic metric mapping (LDDMM). We first exhibit the limited predictive abilities of geodesic regression extrapolation on this group. Building on the recent concept of parallel curves in shape manifolds, we then introduce a second predictive protocol which personalizes previously learned trajectories to new subjects, and investigate the relative performances of two parallel shifting paradigms. This design only requires the baseline imaging data. Finally, coefficients encoding the disease dynamics are obtained from longitudinal cognitive measurements for each subject, and exploited to refine our methodology which is demonstrated to successfully predict the follow-up visits.