Improving Uncertainty-based Out-of-Distribution Detection for Medical Image Segmentation

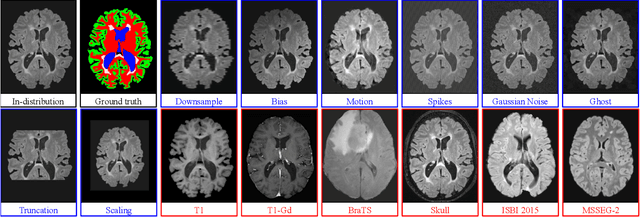
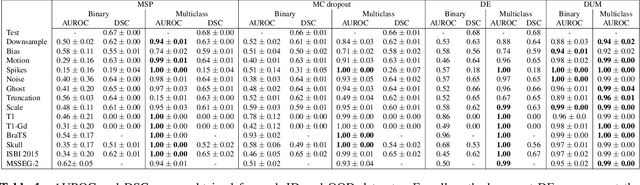
Deep Learning models are easily disturbed by variations in the input images that were not seen during training, resulting in unpredictable behaviours. Such Out-of-Distribution (OOD) images represent a significant challenge in the context of medical image analysis, where the range of possible abnormalities is extremely wide, including artifacts, unseen pathologies, or different imaging protocols. In this work, we evaluate various uncertainty frameworks to detect OOD inputs in the context of Multiple Sclerosis lesions segmentation. By implementing a comprehensive evaluation scheme including 14 sources of OOD of various nature and strength, we show that methods relying on the predictive uncertainty of binary segmentation models often fails in detecting outlying inputs. On the contrary, learning to segment anatomical labels alongside lesions highly improves the ability to detect OOD inputs.

Trustworthy clinical AI solutions: a unified review of uncertainty quantification in deep learning models for medical image analysis

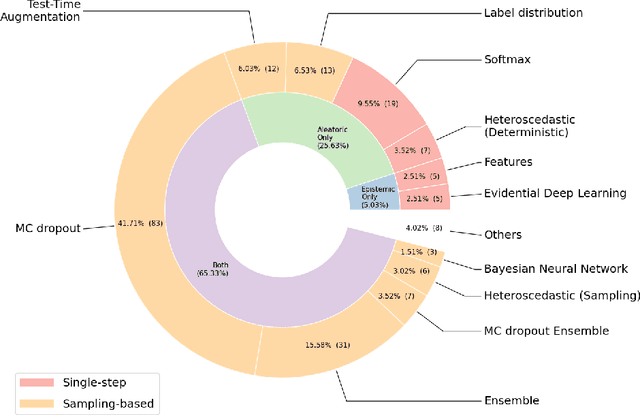
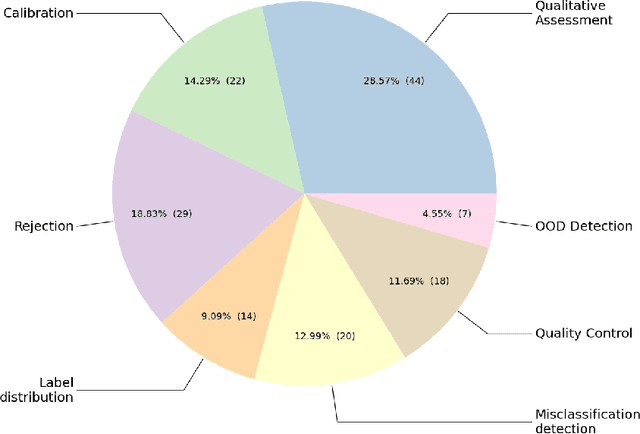
The full acceptance of Deep Learning (DL) models in the clinical field is rather low with respect to the quantity of high-performing solutions reported in the literature. Particularly, end users are reluctant to rely on the rough predictions of DL models. Uncertainty quantification methods have been proposed in the literature as a potential response to reduce the rough decision provided by the DL black box and thus increase the interpretability and the acceptability of the result by the final user. In this review, we propose an overview of the existing methods to quantify uncertainty associated to DL predictions. We focus on applications to medical image analysis, which present specific challenges due to the high dimensionality of images and their quality variability, as well as constraints associated to real-life clinical routine. We then discuss the evaluation protocols to validate the relevance of uncertainty estimates. Finally, we highlight the open challenges of uncertainty quantification in the medical field.

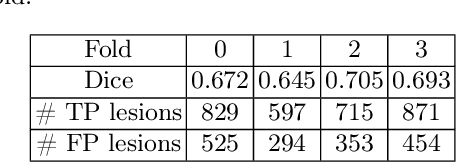
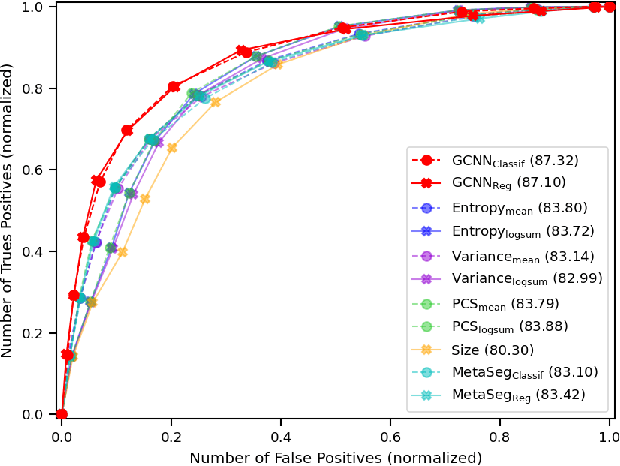
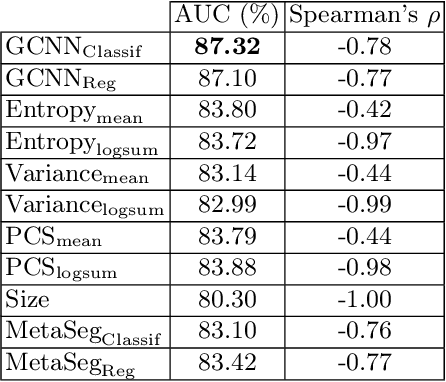
Beyond Voxel Prediction Uncertainty: Identifying brain lesions you can trust

Deep neural networks have become the gold-standard approach for the automated segmentation of 3D medical images. Their full acceptance by clinicians remains however hampered by the lack of intelligible uncertainty assessment of the provided results. Most approaches to quantify their uncertainty, such as the popular Monte Carlo dropout, restrict to some measure of uncertainty in prediction at the voxel level. In addition not to be clearly related to genuine medical uncertainty, this is not clinically satisfying as most objects of interest (e.g. brain lesions) are made of groups of voxels whose overall relevance may not simply reduce to the sum or mean of their individual uncertainties. In this work, we propose to go beyond voxel-wise assessment using an innovative Graph Neural Network approach, trained from the outputs of a Monte Carlo dropout model. This network allows the fusion of three estimators of voxel uncertainty: entropy, variance, and model's confidence; and can be applied to any lesion, regardless of its shape or size. We demonstrate the superiority of our approach for uncertainty estimate on a task of Multiple Sclerosis lesions segmentation.

Leveraging 3D Information in Unsupervised Brain MRI Segmentation

Automatic segmentation of brain abnormalities is challenging, as they vary considerably from one pathology to another. Current methods are supervised and require numerous annotated images for each pathology, a strenuous task. To tackle anatomical variability, Unsupervised Anomaly Detection (UAD) methods are proposed, detecting anomalies as outliers of a healthy model learned using a Variational Autoencoder (VAE). Previous work on UAD adopted a 2D approach, meaning that MRIs are processed as a collection of independent slices. Yet, it does not fully exploit the spatial information contained in MRI. Here, we propose to perform UAD in a 3D fashion and compare 2D and 3D VAEs. As a side contribution, we present a new loss function guarantying a robust training. Learning is performed using a multicentric dataset of healthy brain MRIs, and segmentation performances are estimated on White-Matter Hyperintensities and tumors lesions. Experiments demonstrate the interest of 3D methods which outperform their 2D counterparts.