Jean Feydy
Normalizing Diffusion Kernels with Optimal Transport
Jul 08, 2025Abstract:Smoothing a signal based on local neighborhoods is a core operation in machine learning and geometry processing. On well-structured domains such as vector spaces and manifolds, the Laplace operator derived from differential geometry offers a principled approach to smoothing via heat diffusion, with strong theoretical guarantees. However, constructing such Laplacians requires a carefully defined domain structure, which is not always available. Most practitioners thus rely on simple convolution kernels and message-passing layers, which are biased against the boundaries of the domain. We bridge this gap by introducing a broad class of smoothing operators, derived from general similarity or adjacency matrices, and demonstrate that they can be normalized into diffusion-like operators that inherit desirable properties from Laplacians. Our approach relies on a symmetric variant of the Sinkhorn algorithm, which rescales positive smoothing operators to match the structural behavior of heat diffusion. This construction enables Laplacian-like smoothing and processing of irregular data such as point clouds, sparse voxel grids or mixture of Gaussians. We show that the resulting operators not only approximate heat diffusion but also retain spectral information from the Laplacian itself, with applications to shape analysis and matching.
Accurate Point Cloud Registration with Robust Optimal Transport
Nov 01, 2021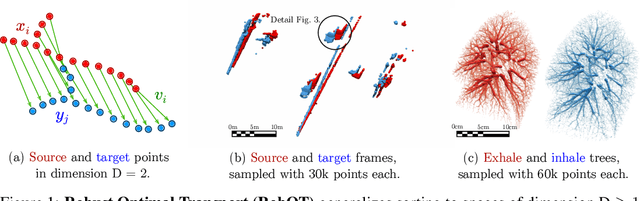
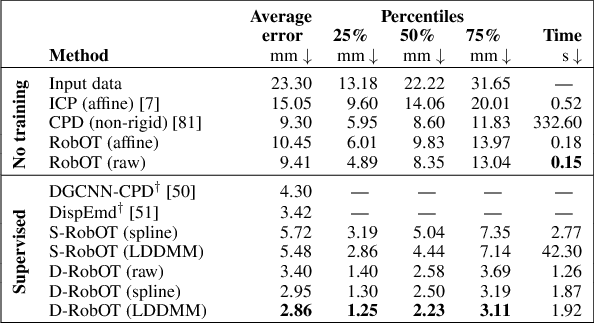
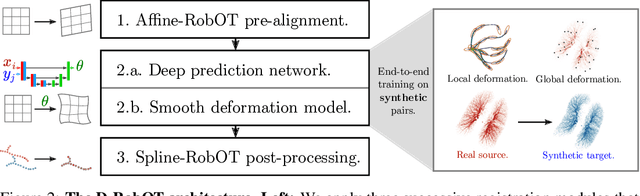
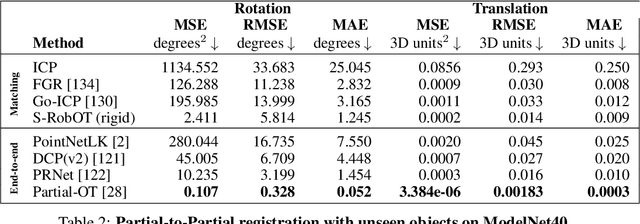
Abstract:This work investigates the use of robust optimal transport (OT) for shape matching. Specifically, we show that recent OT solvers improve both optimization-based and deep learning methods for point cloud registration, boosting accuracy at an affordable computational cost. This manuscript starts with a practical overview of modern OT theory. We then provide solutions to the main difficulties in using this framework for shape matching. Finally, we showcase the performance of transport-enhanced registration models on a wide range of challenging tasks: rigid registration for partial shapes; scene flow estimation on the Kitti dataset; and nonparametric registration of lung vascular trees between inspiration and expiration. Our OT-based methods achieve state-of-the-art results on Kitti and for the challenging lung registration task, both in terms of accuracy and scalability. We also release PVT1010, a new public dataset of 1,010 pairs of lung vascular trees with densely sampled points. This dataset provides a challenging use case for point cloud registration algorithms with highly complex shapes and deformations. Our work demonstrates that robust OT enables fast pre-alignment and fine-tuning for a wide range of registration models, thereby providing a new key method for the computer vision toolbox. Our code and dataset are available online at: https://github.com/uncbiag/robot.
Fast and Scalable Optimal Transport for Brain Tractograms
Jul 05, 2021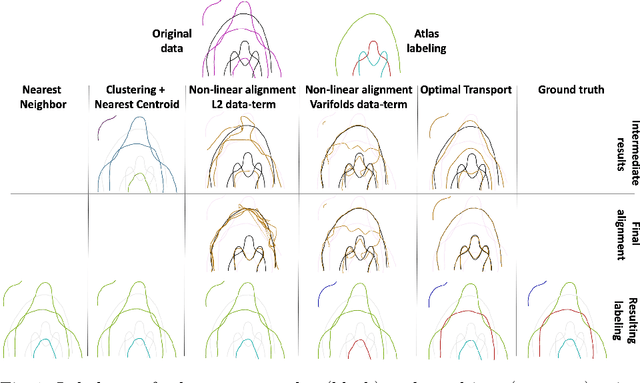

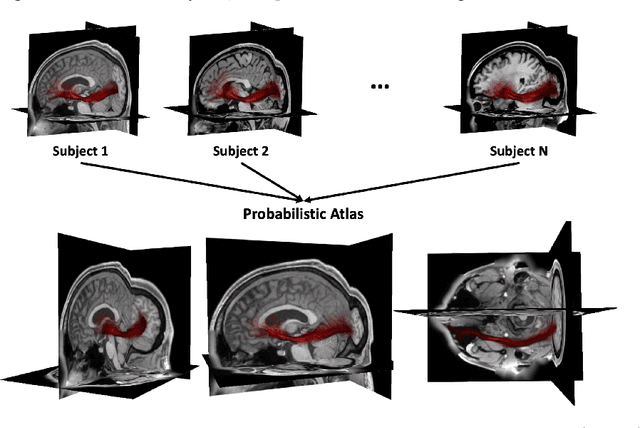
Abstract:We present a new multiscale algorithm for solving regularized Optimal Transport problems on the GPU, with a linear memory footprint. Relying on Sinkhorn divergences which are convex, smooth and positive definite loss functions, this method enables the computation of transport plans between millions of points in a matter of minutes. We show the effectiveness of this approach on brain tractograms modeled either as bundles of fibers or as track density maps. We use the resulting smooth assignments to perform label transfer for atlas-based segmentation of fiber tractograms. The parameters -- blur and reach -- of our method are meaningful, defining the minimum and maximum distance at which two fibers are compared with each other. They can be set according to anatomical knowledge. Furthermore, we also propose to estimate a probabilistic atlas of a population of track density maps as a Wasserstein barycenter. Our CUDA implementation is endowed with a user-friendly PyTorch interface, freely available on the PyPi repository (pip install geomloss) and at www.kernel-operations.io/geomloss.
* MICCAI 2019
Kernel Operations on the GPU, with Autodiff, without Memory Overflows
Mar 27, 2020Abstract:The KeOps library provides a fast and memory-efficient GPU support for tensors whose entries are given by a mathematical formula, such as kernel and distance matrices. KeOps alleviates the major bottleneck of tensor-centric libraries for kernel and geometric applications: memory consumption. It also supports automatic differentiation and outperforms standard GPU baselines, including PyTorch CUDA tensors or the Halide and TVM libraries. KeOps combines optimized C++/CUDA schemes with binders for high-level languages: Python (Numpy and PyTorch), Matlab and GNU R. As a result, high-level "quadratic" codes can now scale up to large data sets with millions of samples processed in seconds. KeOps brings graphics-like performances for kernel methods and is freely available on standard repositories (PyPi, CRAN). To showcase its versatility, we provide tutorials in a wide range of settings online at \url{www.kernel-operations.io}.
Sinkhorn Divergences for Unbalanced Optimal Transport
Oct 28, 2019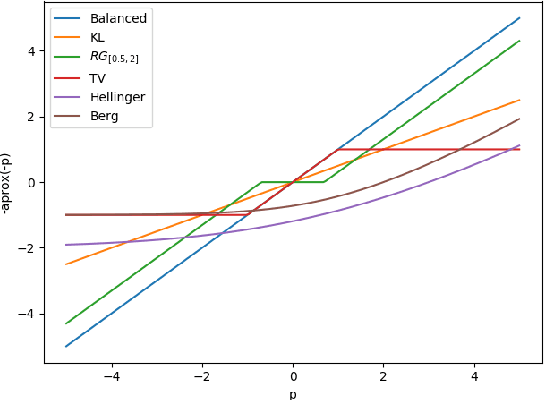
Abstract:This paper extends the formulation of Sinkhorn divergences to the unbalanced setting of arbitrary positive measures, providing both theoretical and algorithmic advances. Sinkhorn divergences leverage the entropic regularization of Optimal Transport (OT) to define geometric loss functions. They are differentiable, cheap to compute and do not suffer from the curse of dimensionality, while maintaining the geometric properties of OT, in particular they metrize the weak$^*$ convergence. Extending these divergences to the unbalanced setting is of utmost importance since most applications in data sciences require to handle both transportation and creation/destruction of mass. This includes for instance problems as diverse as shape registration in medical imaging, density fitting in statistics, generative modeling in machine learning, and particles flows involving birth/death dynamics. Our first set of contributions is the definition and the theoretical analysis of the unbalanced Sinkhorn divergences. They enjoy the same properties as the balanced divergences (classical OT), which are obtained as a special case. Indeed, we show that they are convex, differentiable and metrize the weak$^*$ convergence. Our second set of contributions studies generalized Sinkkhorn iterations, which enable a fast, stable and massively parallelizable algorithm to compute these divergences. We show, under mild assumptions, a linear rate of convergence, independent of the number of samples, i.e. which can cope with arbitrary input measures. We also highlight the versatility of this method, which takes benefit from the latest advances in term of GPU computing, for instance through the KeOps library for fast and scalable kernel operations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge