Fast and Scalable Optimal Transport for Brain Tractograms

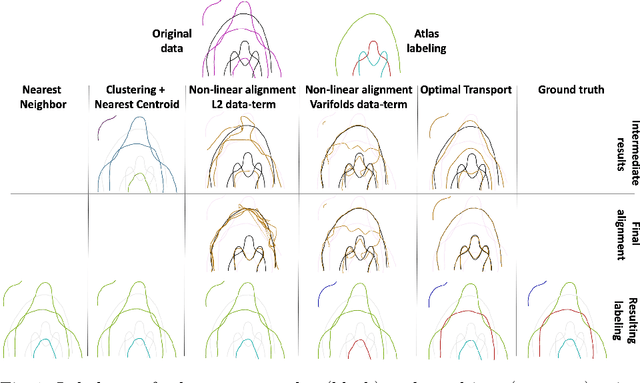
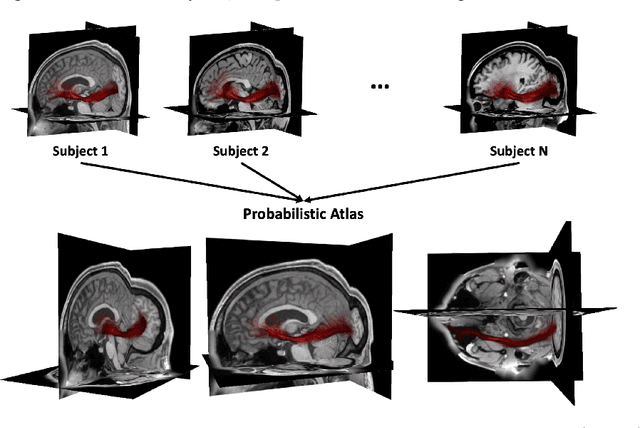
We present a new multiscale algorithm for solving regularized Optimal Transport problems on the GPU, with a linear memory footprint. Relying on Sinkhorn divergences which are convex, smooth and positive definite loss functions, this method enables the computation of transport plans between millions of points in a matter of minutes. We show the effectiveness of this approach on brain tractograms modeled either as bundles of fibers or as track density maps. We use the resulting smooth assignments to perform label transfer for atlas-based segmentation of fiber tractograms. The parameters -- blur and reach -- of our method are meaningful, defining the minimum and maximum distance at which two fibers are compared with each other. They can be set according to anatomical knowledge. Furthermore, we also propose to estimate a probabilistic atlas of a population of track density maps as a Wasserstein barycenter. Our CUDA implementation is endowed with a user-friendly PyTorch interface, freely available on the PyPi repository (pip install geomloss) and at www.kernel-operations.io/geomloss.

Faster Wasserstein Distance Estimation with the Sinkhorn Divergence

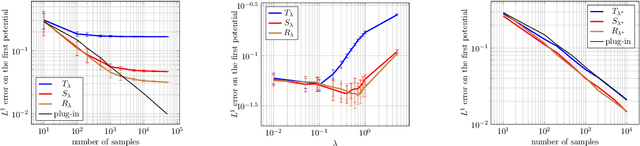
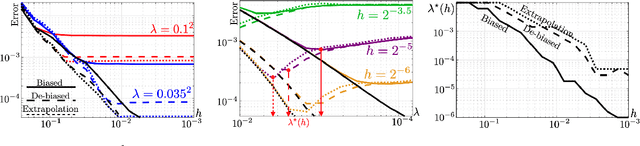
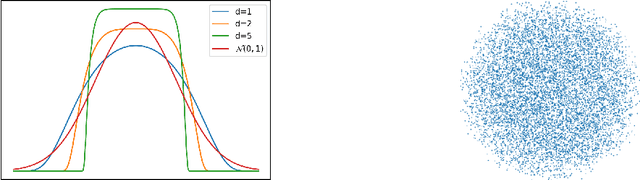
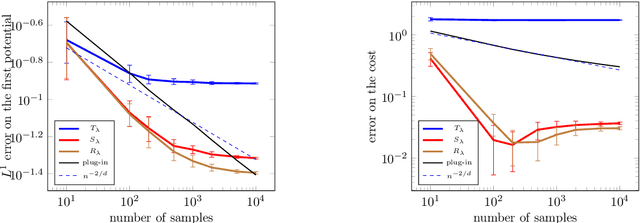
The squared Wasserstein distance is a natural quantity to compare probability distributions in a non-parametric setting. This quantity is usually estimated with the plug-in estimator, defined via a discrete optimal transport problem. It can be solved to $\epsilon$-accuracy by adding an entropic regularization of order $\epsilon$ and using for instance Sinkhorn's algorithm. In this work, we propose instead to estimate it with the Sinkhorn divergence, which is also built on entropic regularization but includes debiasing terms. We show that, for smooth densities, this estimator has a comparable sample complexity but allows higher regularization levels, of order $\epsilon^{1/2}$ , which leads to improved computational complexity bounds and a strong speedup in practice. Our theoretical analysis covers the case of both randomly sampled densities and deterministic discretizations on uniform grids. We also propose and analyze an estimator based on Richardson extrapolation of the Sinkhorn divergence which enjoys improved statistical and computational efficiency guarantees, under a condition on the regularity of the approximation error, which is in particular satisfied for Gaussian densities. We finally demonstrate the efficiency of the proposed estimators with numerical experiments.