Mirror Descent with Relative Smoothness in Measure Spaces, with application to Sinkhorn and EM

Many problems in machine learning can be formulated as optimizing a convex functional over a space of measures. This paper studies the convergence of the mirror descent algorithm in this infinite-dimensional setting. Defining Bregman divergences through directional derivatives, we derive the convergence of the scheme for relatively smooth and strongly convex pairs of functionals. Applying our result to joint distributions and the Kullback--Leibler (KL) divergence, we show that Sinkhorn's primal iterations for entropic optimal transport in the continuous setting correspond to a mirror descent, and we obtain a new proof of its (sub)linear convergence. We also show that Expectation Maximization (EM) can always formally be written as a mirror descent, and, when optimizing on the latent distribution while fixing the mixtures, we derive sublinear rates of convergence.

Faster Wasserstein Distance Estimation with the Sinkhorn Divergence

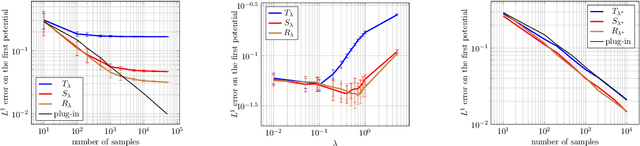
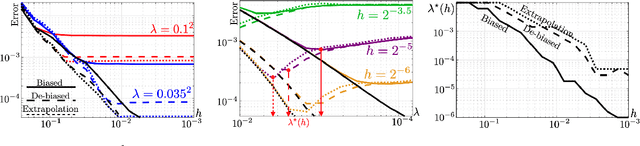
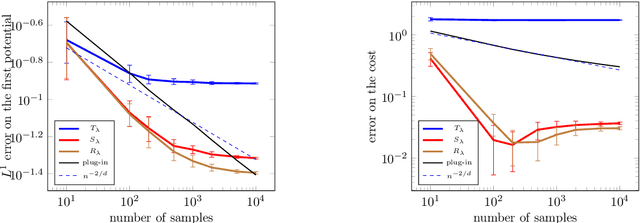
The squared Wasserstein distance is a natural quantity to compare probability distributions in a non-parametric setting. This quantity is usually estimated with the plug-in estimator, defined via a discrete optimal transport problem. It can be solved to $\epsilon$-accuracy by adding an entropic regularization of order $\epsilon$ and using for instance Sinkhorn's algorithm. In this work, we propose instead to estimate it with the Sinkhorn divergence, which is also built on entropic regularization but includes debiasing terms. We show that, for smooth densities, this estimator has a comparable sample complexity but allows higher regularization levels, of order $\epsilon^{1/2}$ , which leads to improved computational complexity bounds and a strong speedup in practice. Our theoretical analysis covers the case of both randomly sampled densities and deterministic discretizations on uniform grids. We also propose and analyze an estimator based on Richardson extrapolation of the Sinkhorn divergence which enjoys improved statistical and computational efficiency guarantees, under a condition on the regularity of the approximation error, which is in particular satisfied for Gaussian densities. We finally demonstrate the efficiency of the proposed estimators with numerical experiments.

Efficient Matrix Completion with Gaussian Models

A general framework based on Gaussian models and a MAP-EM algorithm is introduced in this paper for solving matrix/table completion problems. The numerical experiments with the standard and challenging movie ratings data show that the proposed approach, based on probably one of the simplest probabilistic models, leads to the results in the same ballpark as the state-of-the-art, at a lower computational cost.