The fshape framework for the variability analysis of functional shapes
Paper and Code
Apr 24, 2014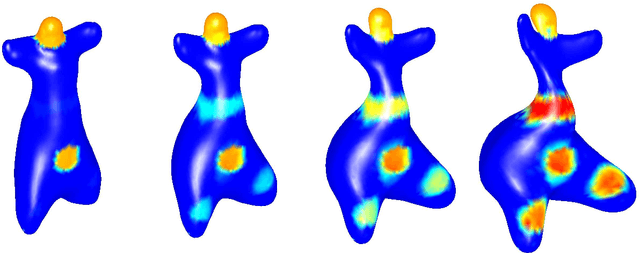
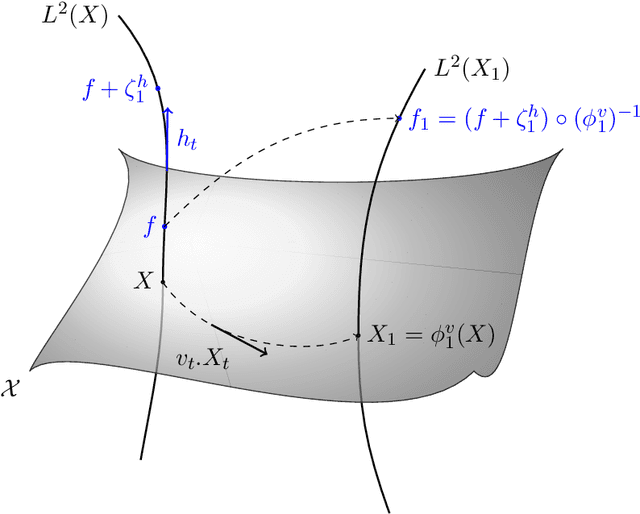
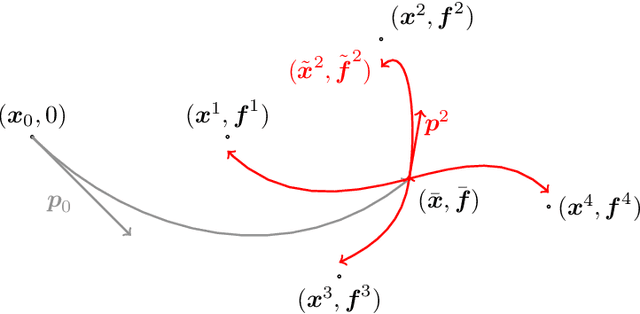
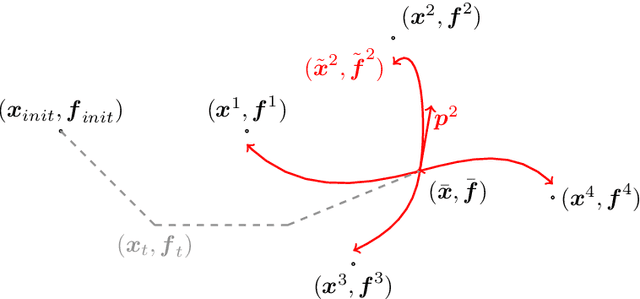
This article introduces a full mathematical and numerical framework for treating functional shapes (or fshapes) following the landmarks of shape spaces and shape analysis. Functional shapes can be described as signal functions supported on varying geometrical supports. Analysing variability of fshapes' ensembles require the modelling and quantification of joint variations in geometry and signal, which have been treated separately in previous approaches. Instead, building on the ideas of shape spaces for purely geometrical objects, we propose the extended concept of fshape bundles and define Riemannian metrics for fshape metamorphoses to model geometrico-functional transformations within these bundles. We also generalize previous works on data attachment terms based on the notion of varifolds and demonstrate the utility of these distances. Based on these, we propose variational formulations of the atlas estimation problem on populations of fshapes and prove existence of solutions for the different models. The second part of the article examines the numerical implementation of the models by detailing discrete expressions for the metrics and gradients and proposing an optimization scheme for the atlas estimation problem. We present a few results of the methodology on a synthetic dataset as well as on a population of retinal membranes with thickness maps.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge