Match and Reweight Strategy for Generalized Target Shift
Paper and Code
Jun 15, 2020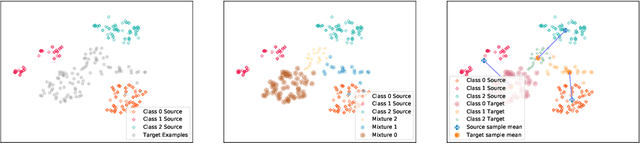
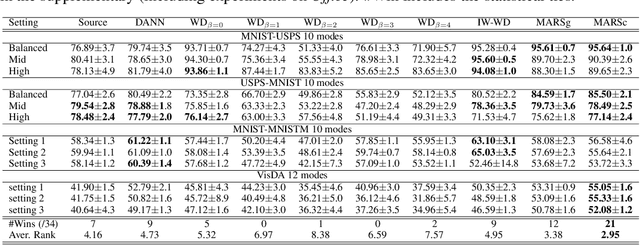
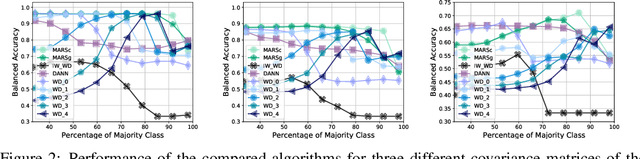
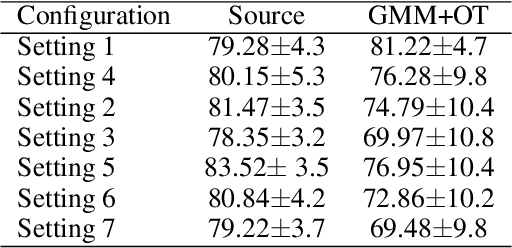
We address the problem of unsupervised domain adaptation under the setting of generalized target shift (both class-conditional and label shifts occur). We show that in that setting, for good generalization, it is necessary to learn with similar source and target label distributions and to match the class-conditional probabilities. For this purpose, we propose an estimation of target label proportion by blending mixture estimation and optimal transport. This estimation comes with theoretical guarantees of correctness. Based on the estimation, we learn a model by minimizing a importance weighted loss and a Wasserstein distance between weighted marginals. We prove that this minimization allows to match class-conditionals given mild assumptions on their geometry. Our experimental results show that our method performs better on average than competitors accross a range domain adaptation problems including digits,VisDA and Office.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge