Time Series Alignment with Global Invariances

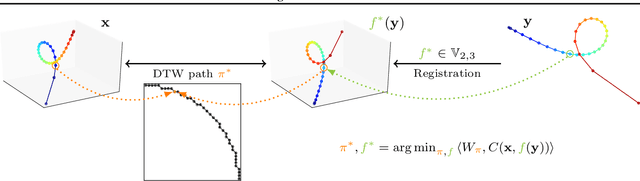
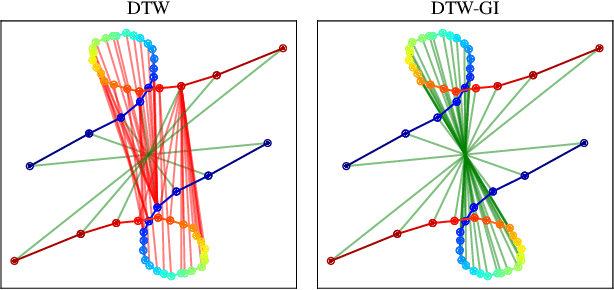
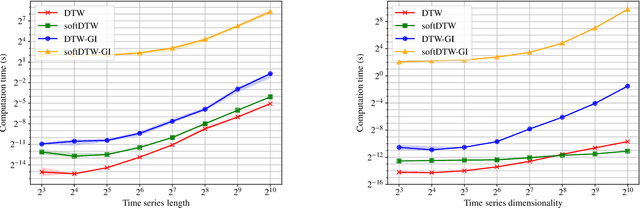
In this work we address the problem of comparing time series while taking into account both feature space transformation and temporal variability. The proposed framework combines a latent global transformation of the feature space with the widely used Dynamic Time Warping (DTW). The latent global transformation captures the feature invariance while the DTW (or its smooth counterpart soft-DTW) deals with the temporal shifts. We cast the problem as a joint optimization over the global transformation and the temporal alignments. The versatility of our framework allows for several variants depending on the invariance class at stake. Among our contributions we define a differentiable loss for time series and present two algorithms for the computation of time series barycenters under our new geometry. We illustrate the interest of our approach on both simulated and real world data.