Sliced Gromov-Wasserstein
Paper and Code
May 24, 2019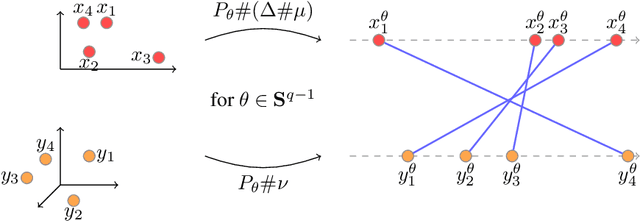
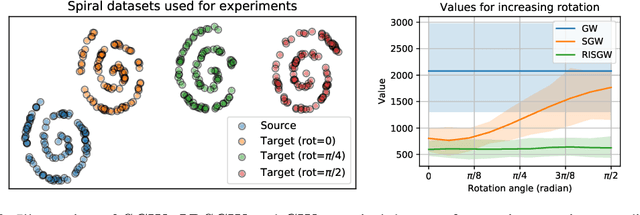
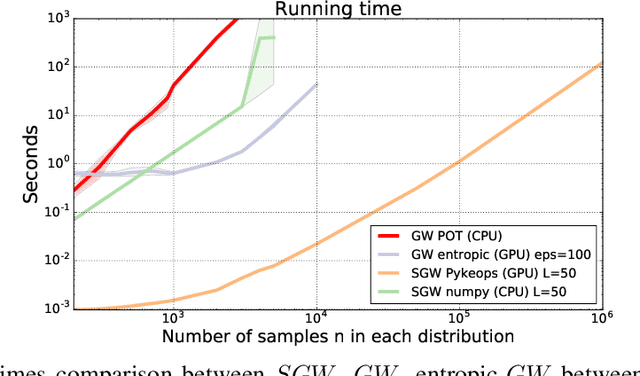
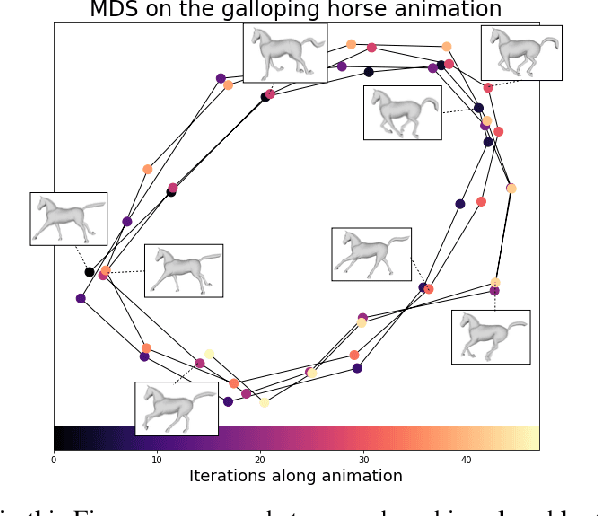
Recently used in various machine learning contexts, the Gromov-Wasserstein distance (GW) allows for comparing distributions that do not necessarily lie in the same metric space. However, this Optimal Transport (OT) distance requires solving a complex non convex quadratic program which is most of the time very costly both in time and memory. Contrary to GW, the Wasserstein distance (W) enjoys several properties (e.g. duality) that permit large scale optimization. Among those, the Sliced Wasserstein (SW) distance exploits the direct solution of W on the line, that only requires sorting discrete samples in 1D. This paper propose a new divergence based on GW akin to SW. We first derive a closed form for GW when dealing with 1D distributions, based on a new result for the related quadratic assignment problem. We then define a novel OT discrepancy that can deal with large scale distributions via a slicing approach and we show how it relates to the GW distance while being $O(n^2)$ to compute. We illustrate the behavior of this so called Sliced Gromov-Wasserstein (SGW) discrepancy in experiments where we demonstrate its ability to tackle similar problems as GW while being several order of magnitudes faster to compute
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge