Fast Optimal Transport through Sliced Wasserstein Generalized Geodesics
Paper and Code
Jul 04, 2023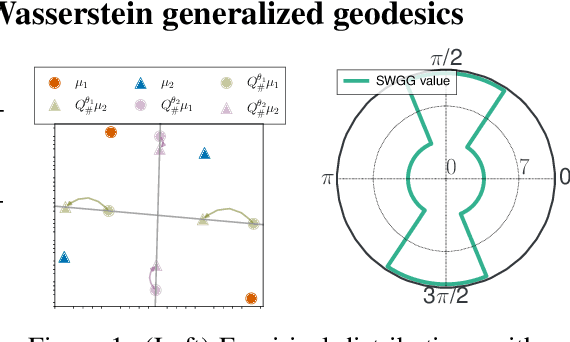

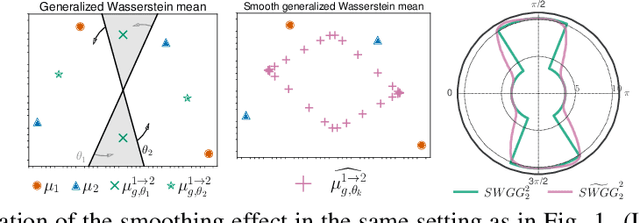
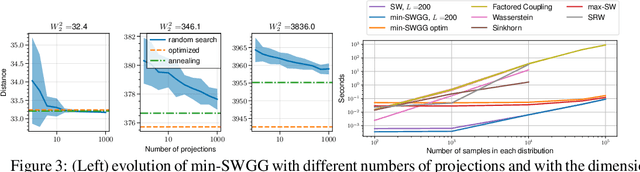
Wasserstein distance (WD) and the associated optimal transport plan have been proven useful in many applications where probability measures are at stake. In this paper, we propose a new proxy of the squared WD, coined min-SWGG, that is based on the transport map induced by an optimal one-dimensional projection of the two input distributions. We draw connections between min-SWGG and Wasserstein generalized geodesics in which the pivot measure is supported on a line. We notably provide a new closed form for the exact Wasserstein distance in the particular case of one of the distributions supported on a line allowing us to derive a fast computational scheme that is amenable to gradient descent optimization. We show that min-SWGG is an upper bound of WD and that it has a complexity similar to as Sliced-Wasserstein, with the additional feature of providing an associated transport plan. We also investigate some theoretical properties such as metricity, weak convergence, computational and topological properties. Empirical evidences support the benefits of min-SWGG in various contexts, from gradient flows, shape matching and image colorization, among others.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge