Fused Gromov-Wasserstein distance for structured objects: theoretical foundations and mathematical properties
Paper and Code
Nov 07, 2018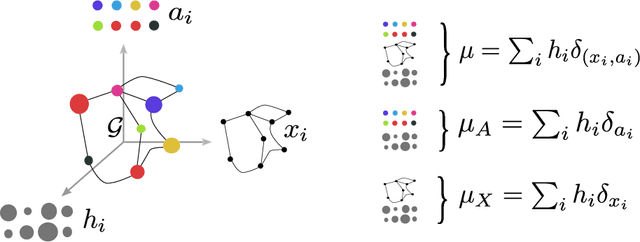


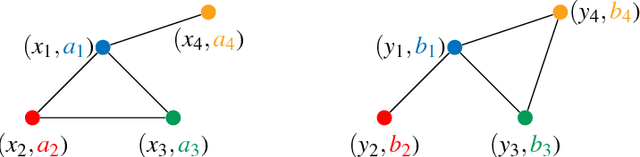
Optimal transport theory has recently found many applications in machine learning thanks to its capacity for comparing various machine learning objects considered as distributions. The Kantorovitch formulation, leading to the Wasserstein distance, focuses on the features of the elements of the objects but treat them independently, whereas the Gromov-Wasserstein distance focuses only on the relations between the elements, depicting the structure of the object, yet discarding its features. In this paper we propose to extend these distances in order to encode simultaneously both the feature and structure informations, resulting in the Fused Gromov-Wasserstein distance. We develop the mathematical framework for this novel distance, prove its metric and interpolation properties and provide a concentration result for the convergence of finite samples. We also illustrate and interpret its use in various contexts where structured objects are involved.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge