Box for Mask and Mask for Box: weak losses for multi-task partially supervised learning

Object detection and semantic segmentation are both scene understanding tasks yet they differ in data structure and information level. Object detection requires box coordinates for object instances while semantic segmentation requires pixel-wise class labels. Making use of one task's information to train the other would be beneficial for multi-task partially supervised learning where each training example is annotated only for a single task, having the potential to expand training sets with different-task datasets. This paper studies various weak losses for partially annotated data in combination with existing supervised losses. We propose Box-for-Mask and Mask-for-Box strategies, and their combination BoMBo, to distil necessary information from one task annotations to train the other. Ablation studies and experimental results on VOC and COCO datasets show favorable results for the proposed idea. Source code and data splits can be found at https://github.com/lhoangan/multas.

Joint multi-modal Self-Supervised pre-training in Remote Sensing: Application to Methane Source Classification

With the current ubiquity of deep learning methods to solve computer vision and remote sensing specific tasks, the need for labelled data is growing constantly. However, in many cases, the annotation process can be long and tedious depending on the expertise needed to perform reliable annotations. In order to alleviate this need for annotations, several self-supervised methods have recently been proposed in the literature. The core principle behind these methods is to learn an image encoder using solely unlabelled data samples. In earth observation, there are opportunities to exploit domain-specific remote sensing image data in order to improve these methods. Specifically, by leveraging the geographical position associated with each image, it is possible to cross reference a location captured from multiple sensors, leading to multiple views of the same locations. In this paper, we briefly review the core principles behind so-called joint-embeddings methods and investigate the usage of multiple remote sensing modalities in self-supervised pre-training. We evaluate the final performance of the resulting encoders on the task of methane source classification.

Spherical Sliced-Wasserstein

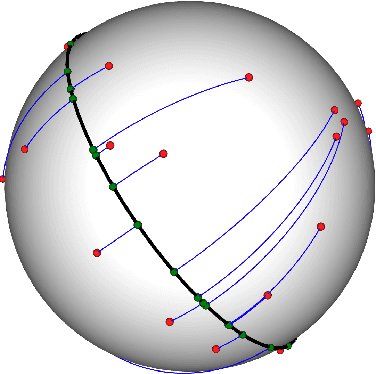
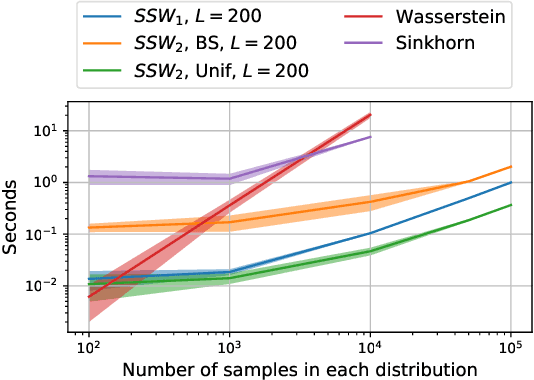
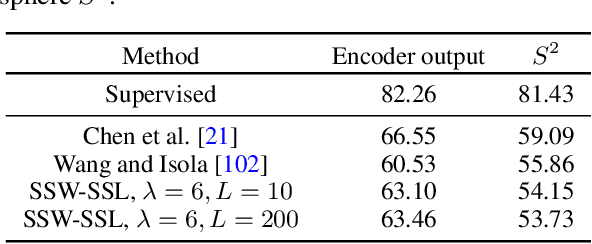
Many variants of the Wasserstein distance have been introduced to reduce its original computational burden. In particular the Sliced-Wasserstein distance (SW), which leverages one-dimensional projections for which a closed-form solution of the Wasserstein distance is available, has received a lot of interest. Yet, it is restricted to data living in Euclidean spaces, while the Wasserstein distance has been studied and used recently on manifolds. We focus more specifically on the sphere, for which we define a novel SW discrepancy, which we call spherical Sliced-Wasserstein, making a first step towards defining SW discrepancies on manifolds. Our construction is notably based on closed-form solutions of the Wasserstein distance on the circle, together with a new spherical Radon transform. Along with efficient algorithms and the corresponding implementations, we illustrate its properties in several machine learning use cases where spherical representations of data are at stake: density estimation on the sphere, variational inference or hyperspherical auto-encoders.