Spherical Sliced-Wasserstein

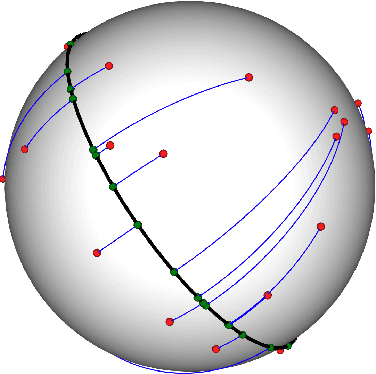
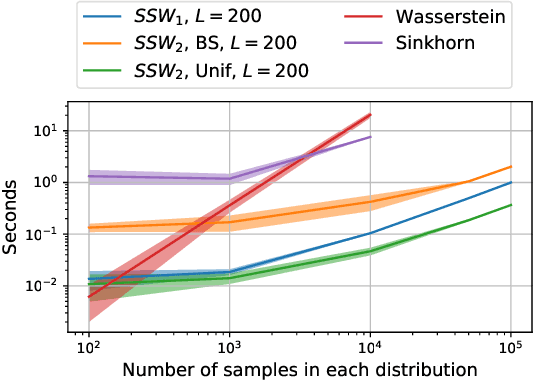
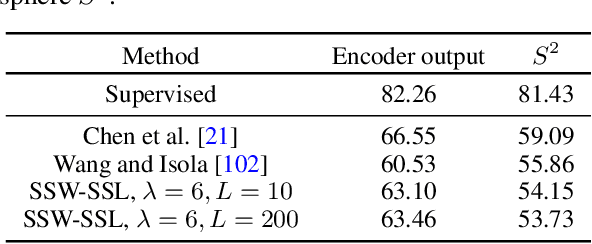
Many variants of the Wasserstein distance have been introduced to reduce its original computational burden. In particular the Sliced-Wasserstein distance (SW), which leverages one-dimensional projections for which a closed-form solution of the Wasserstein distance is available, has received a lot of interest. Yet, it is restricted to data living in Euclidean spaces, while the Wasserstein distance has been studied and used recently on manifolds. We focus more specifically on the sphere, for which we define a novel SW discrepancy, which we call spherical Sliced-Wasserstein, making a first step towards defining SW discrepancies on manifolds. Our construction is notably based on closed-form solutions of the Wasserstein distance on the circle, together with a new spherical Radon transform. Along with efficient algorithms and the corresponding implementations, we illustrate its properties in several machine learning use cases where spherical representations of data are at stake: density estimation on the sphere, variational inference or hyperspherical auto-encoders.

State space partitioning based on constrained spectral clustering for block particle filtering

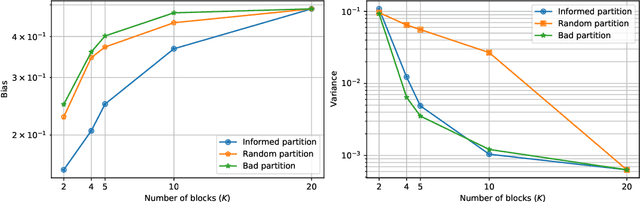
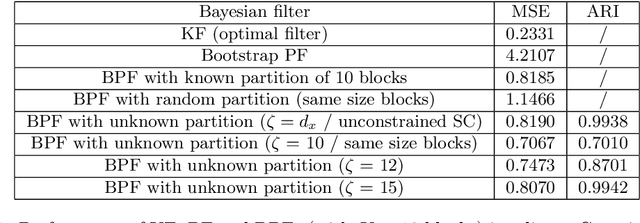
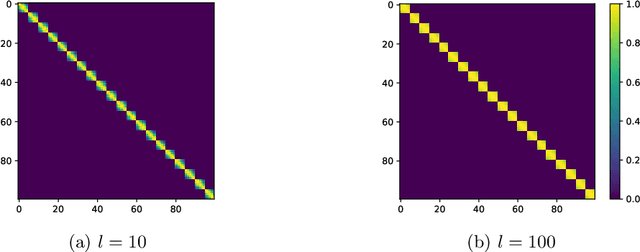
The particle filter (PF) is a powerful inference tool widely used to estimate the filtering distribution in non-linear and/or non-Gaussian problems. To overcome the curse of dimensionality of PF, the block PF (BPF) inserts a blocking step to partition the state space into several subspaces or blocks of smaller dimension so that the correction and resampling steps can be performed independently on each subspace. Using blocks of small size reduces the variance of the filtering distribution estimate, but in turn the correlation between blocks is broken and a bias is introduced. When the dependence relationships between state variables are unknown, it is not obvious to decide how to split the state space into blocks and a significant error overhead may arise from a poor choice of partitioning. In this paper, we formulate the partitioning problem in the BPF as a clustering problem and we propose a state space partitioning method based on spectral clustering (SC). We design a generalized BPF algorithm that contains two new steps: (i) estimation of the state vector correlation matrix from predicted particles, (ii) SC using this estimate as the similarity matrix to determine an appropriate partition. In addition, a constraint is imposed on the maximal cluster size to prevent SC from providing too large blocks. We show that the proposed method can bring together in the same blocks the most correlated state variables while successfully escaping the curse of dimensionality.

Sliced-Wasserstein Gradient Flows

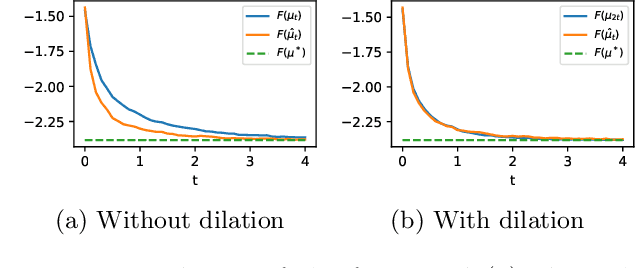
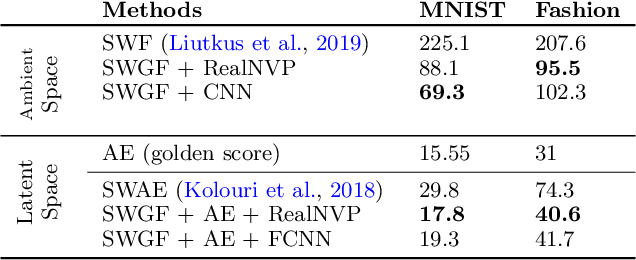
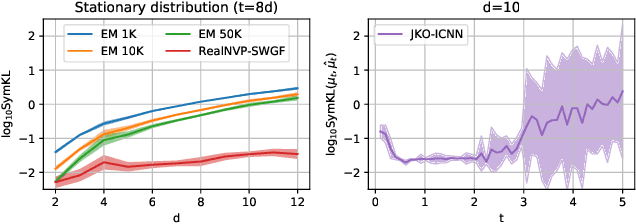
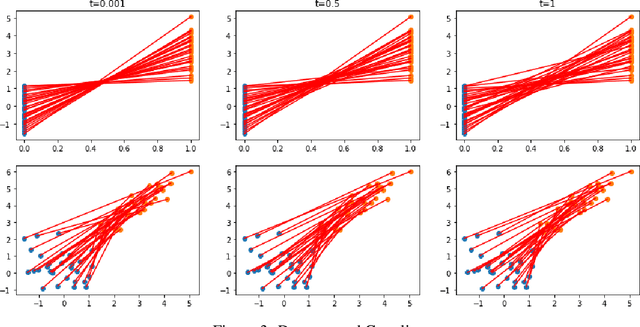
Minimizing functionals in the space of probability distributions can be done with Wasserstein gradient flows. To solve them numerically, a possible approach is to rely on the Jordan-Kinderlehrer-Otto (JKO) scheme which is analogous to the proximal scheme in Euclidean spaces. However, this bilevel optimization problem is known for its computational challenges, especially in high dimension. To alleviate it, very recent works propose to approximate the JKO scheme leveraging Brenier's theorem, and using gradients of Input Convex Neural Networks to parameterize the density (JKO-ICNN). However, this method comes with a high computational cost and stability issues. Instead, this work proposes to use gradient flows in the space of probability measures endowed with the sliced-Wasserstein (SW) distance. We argue that this method is more flexible than JKO-ICNN, since SW enjoys a closed-form differentiable approximation. Thus, the density at each step can be parameterized by any generative model which alleviates the computational burden and makes it tractable in higher dimensions. Interestingly, we also show empirically that these gradient flows are strongly related to the usual Wasserstein gradient flows, and that they can be used to minimize efficiently diverse machine learning functionals.

Subspace Detours Meet Gromov-Wasserstein

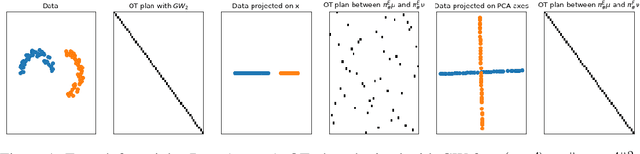
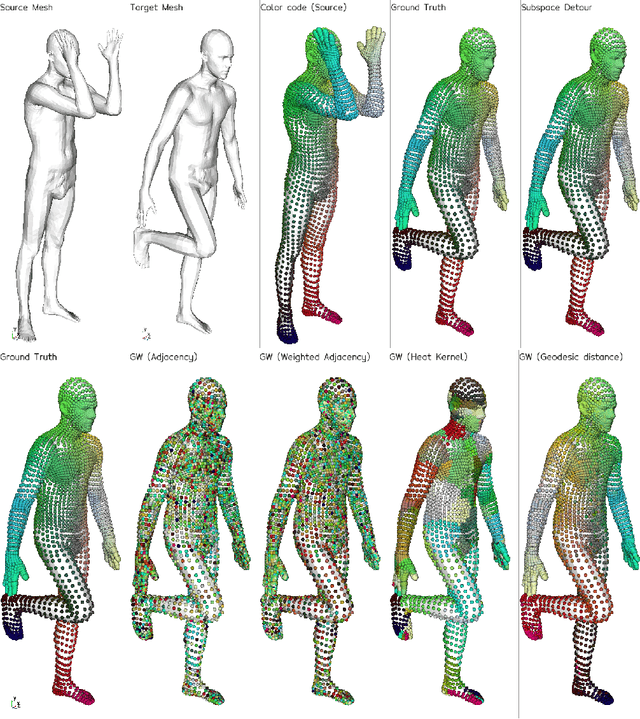
In the context of optimal transport methods, the subspace detour approach was recently presented by Muzellec and Cuturi (2019). It consists in building a nearly optimal transport plan in the measures space from an optimal transport plan in a wisely chosen subspace, onto which the original measures are projected. The contribution of this paper is to extend this category of methods to the Gromov-Wasserstein problem, which is a particular type of transport distance involving the inner geometry of the compared distributions. After deriving the associated formalism and properties, we also discuss a specific cost for which we can show connections with the Knothe-Rosenblatt rearrangement. We finally give an experimental illustration on a shape matching problem.