State space partitioning based on constrained spectral clustering for block particle filtering
Paper and Code
Mar 07, 2022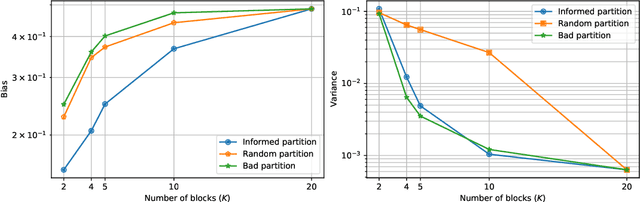
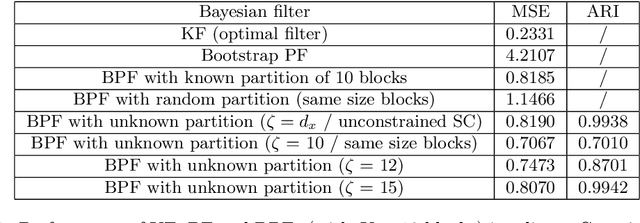
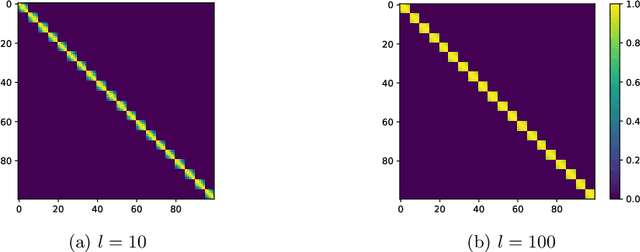

The particle filter (PF) is a powerful inference tool widely used to estimate the filtering distribution in non-linear and/or non-Gaussian problems. To overcome the curse of dimensionality of PF, the block PF (BPF) inserts a blocking step to partition the state space into several subspaces or blocks of smaller dimension so that the correction and resampling steps can be performed independently on each subspace. Using blocks of small size reduces the variance of the filtering distribution estimate, but in turn the correlation between blocks is broken and a bias is introduced. When the dependence relationships between state variables are unknown, it is not obvious to decide how to split the state space into blocks and a significant error overhead may arise from a poor choice of partitioning. In this paper, we formulate the partitioning problem in the BPF as a clustering problem and we propose a state space partitioning method based on spectral clustering (SC). We design a generalized BPF algorithm that contains two new steps: (i) estimation of the state vector correlation matrix from predicted particles, (ii) SC using this estimate as the similarity matrix to determine an appropriate partition. In addition, a constraint is imposed on the maximal cluster size to prevent SC from providing too large blocks. We show that the proposed method can bring together in the same blocks the most correlated state variables while successfully escaping the curse of dimensionality.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge